1.Categories
Generic programming in Mathemagix is based on
the notion of a category. When writing generic functions
(also called templates) or classes (also called containers), it is
usually necessary to make assumptions on the type parameters.
Consider for instance the container Polynomial
R for univariate polynomials. It is natural to use
an internal representation for which the leading coefficient is non
zero. The mere existence of an instance “zero” of type R constitutes a condition
on R. Similarly, the
ring operations on polynomials are naturally defined in terms of the
ring operations on coefficients in R.
Hence, R should at
least be a ring (even though more structure might be needed for
certain operations, such as the computation of greatest common
divisors).
Categories are defined using the following syntax:
category Category_Name == category_body; |
The body of a category consists of a block of prototypes of
functionality required by the category. For instance, a typical
definition of the Ring category is the following:
category Ring == {
convert: Int -> This;
prefix -: This -> This;
infix +: (This, This) -> This;
infix -: (This, This) -> This;
infix *: (This, This) -> This;
} |
The special type This corresponds to the carrier of the
category. A type T is
said to satisfy the category Category_Name in a given context (and we
write T: Category_Name)
if the context provides the required functionality in the body of the
category, with This
replaced by T. In a
context where basix/fundamental.mmx has been included,
we thus have Int: Ring,
since the context provides us with operations
convert: Int -> Int;
prefix -: Int -> Int;
infix +: (Int, Int) -> Int;
infix -: (Int, Int) -> Int;
infix *: (Int, Int) -> Int; |
However, we do not have String:
Ring, since there is no implementation of infix - on strings.
2.Mathematical properties
It should be noticed that the notion of category satisfaction is
purely syntactic: we simply look whether all prototypes in the body of
the category are implemented in the current context, but we do not
check any of the customary properties that the names of the category
might suggest. For example, the type Double
satisfies the category Ring,
since the operations
convert: Int -> Double;
prefix -: Double -> Double;
infix +: (Double, Double) -> Double;
infix -: (Double, Double) -> Double;
infix *: (Double, Double) -> Double; |
are all defined in basix/double.mmx. However, these
operations are not associative: we typically have (1.0e100 + 1.0) - 1.0e100 != 1.0, due to
rounding errors.
From the programming point of view this is really a feature, since it
is desirable that straightforward implementations of containers such
as Polynomial R can be
instantiated for R  Double.
However, from the mathematical point of view, the code cannot
certified to be correct under all circumstances.
Double.
However, from the mathematical point of view, the code cannot
certified to be correct under all circumstances.
Since Mathemagix aims to be an efficient general
purpose mathematical programmer language rather than an automatic
theorem prover, we have integrated no support for checking
mathematical relations. Nevertheless, nothing prevents the user to
informally introduce dummy functions which correspond to mathematical
properties which are intended to be satisfied. For instance, the user
might replace the definition of a ring by something like
category Ring == {
convert: Int -> This;
prefix -: This -> This;
infix +: (This, This) -> This;
infix -: (This, This) -> This;
infix *: (This, This) -> This;
associative_addition: This -> Void;
commutative_addition: This -> Void;
additive_inverse: This -> Void;
associative_multiplication: This -> Void;
…
} |
The idea is that each of these additional functions stands for a
mathematical property. For instance, associative_addition
would stand for the property that 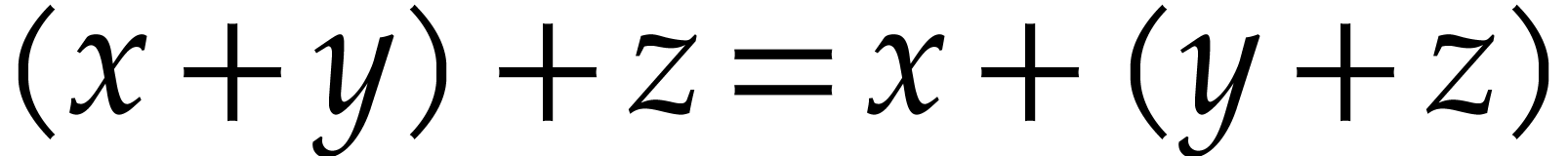 for all
for all 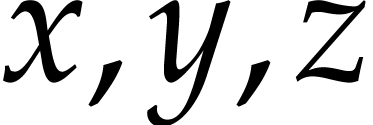 in the carrier. A dummy implementation
in the carrier. A dummy implementation
associative_addition (x: T): Void == {} |
of associative_addition
corresponds to the assertion that the corresponding mathematical
property is satisfied for T.
However, this assertion is not checked by the compiler, and simply
admitted on good faith.
3.Inheritance
It frequently happens that we want to declare new categories which are
really extensions of already existing categories. For instance, the
following category Field is really the extension of the category Ring with a division:
category Field == {
convert: Int -> This;
prefix -: This -> This;
infix +: (This, This) -> This;
infix -: (This, This) -> This;
infix *: (This, This) -> This;
infix /: (This, This) -> This;
} |
A shorter and more comprehensive way to define this category is
category Field == {
This: Ring;
infix /: (This, This) -> This;
} |
In other words, in our specification of the functionality of
categories, we allow for prototypes of the form
which really correspond to inheriting all functionality from another
category. Multiple inheritance is allowed in the same way. For
instance, assuming
category Ordered == {
infix <=: (This, This) -> Boolean;
} |
we may define
category Ordered_Ring == {
This: Ring;
This: Ordered;
} |
4.Parameterized
categories
Categories are allowed to be parameterized. The syntax for defining
parameterized categories is similar to the syntax for the definition
of containers:
category Cat (Param_1: Type_1, …, Param_n: Type_n) == category_body |
The parameters are allowed to depend on each other in an arbitrary
order, although cyclic dependencies are not allowed. The parameters
may either be types or ordinary values.
Two examples of parameterized categories To
F and From
T were already encountered in the section on type converters:
category To (T: Type) == {
convert: This -> T;
} |
category From (F: Type) == {
convert: F -> This;
} |
Another typical example of a parameterized category is
category Vector_Space (K: Field) == {
This: Abelian_Group;
infix *: (K, This) -> This;
} |
5.Planned extensions
One planned extension for categories concerns default implementations
of certain methods. For instance, in the category Ring, the operation infix - is really redundant, since it
admits a reasonable default implementation
infix - (x: This, y: This): This == x + (-y); |
In the future, Mathemagix should be able to use
such default implementations except when a better method is explicitly
provided by the user. Notice that this requires a mechanism for
specifying the required functionality for default methods. This is not
completely trivial, since it should also be possible to provide a
default implementation of prefix
- in terms of infix
-:
prefix - (x: This): This == (0 :> This) - x; |
Of course, this should not lead to infinite loops if neither prefix - nor infix - is present.
6.Efficiency considerations
© 2012 Joris van der Hoeven
Permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU General Public License. If you
don't have this file, write to the Free Software Foundation, Inc., 59
Temple Place - Suite 330, Boston, MA 02111-1307, USA.
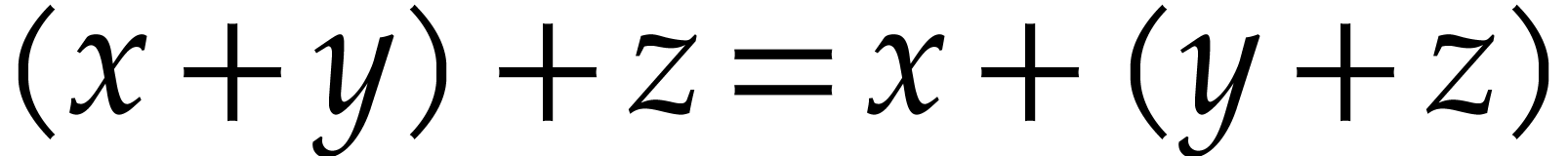 for all
for all 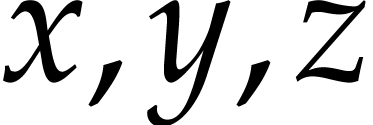 in the carrier. A dummy implementation
in the carrier. A dummy implementation