1.Declaration
of new classes
The user may define new classes using the keyword class. A simple
example of a user defined class is the following:
class Point == {
x: Double;
y: Double;
constructor point (x2: Double, y2: Double) == {
x == x2;
y == y2;
}
} |
Declarations of variables inside the class correspond to declarations
of the internal data fields of that class. In addition, it is possible
to define constructors, destructors and methods (also called member
functions).
2.Data fields
Declarations of variables inside the class correspond to declarations
of data fields for that class. The data field with name x can be accessed using the postfix
operator .x. For
instance, we may define an addition on points as follows:
infix + (p: Point, q: Point): Point == point (p.x + q.x, p.y + q.y); |
By default, data fields are read only. They can be made read-write
using the keyword mutable, as in the following example:
class Point == {
mutable {
x: Double;
y: Double;
}
constructor point (x2: Double, y2: Double) == {
x == x2;
y == y2;
}
} |
Assuming the above definition, the following code would be correct:
translate (p: Alias Point, q: Point): Void == {
p.x := p.x + q.x;
p.y := p.y + q.y;
} |
Notice that the user may define additional postfix operators of the
form .name outside the
class, which will behave in a similar way as actual data fields. For
instance, defining
postfix .length (p: Point): Double == sqrt (square p.x + square p.y); |
we may write
mmout << point (3.0, 4.0).length << lf; |
3.Constructors
and destructors
In order to be useful, a user defined class should at least provide
one constructor. By convention, constructors usually carry the same
name as the class, in lowercase. For instance, in the above example,
the unique constructor for the class Point
carried the name point.
Nevertheless, the user is free to choose any other name.
In the body of the constructor, the user should provide values for
each of the data fields of the class, while preserving the ordering of
declarations. Constructors are also required to be defined inside the
class itself. Nevertheless, the function name of the constructor can
be overloaded outside the class. For instance, we may very well define
the function
point (): Point == point (0.0, 0.0); |
outside the class, which behaves as if it were a constructor.
The default destructors for class instances are usually what the user
wants in Mathemagix, except when some special
action needs to be undertaken when an instance is destroyed (such as
saving some data to a file before destruction). Destructors are
defined as functions with no arguments and no return type using the
keyword destructor. For instance, the following modification of the class Point allows the user to
monitor when points are destroyed:
class Point == {
x: Double;
y: Double;
constructor point (x2: Double, y2: Double) == {
x == x2;
y == y2;
}
destructor () == {
mmout << "Destroying " << x << ", " << y << lf;
}
} |
4.Methods
Special methods on class instances can be defined inside the class
using the keyword method. For instance, a method for transposing the 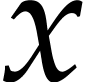 and
and 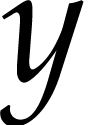 coordinates might be defined as follows:
coordinates might be defined as follows:
class Point == {
x: Double;
y: Double;
constructor point (x2: Double, y2: Double) == {
x == x2;
y == y2;
}
method reflect (): Point == point (y, x);
} |
We may apply the method using the postfix operator .reflect:
mmout << point (1.0, 2.0).reflect () << lf; |
Inside the body of a method, we notice that the data fields of the
class can be accessed without specifying the instance, which is
implicit. For instance, inside the definition of reflect, we were allowed to write point (y, x) instead of point (this.y, this.x),
where this
corresponds to the underlying instance which is implicit. Similarly,
other methods can be called without the need to specify the underlying
instance.
5.Containers
Containers such as vectors or matrices can also be declared using the
class
keyword, using the syntax
class Container (Param_1: Type_1, …, Param_n: Type_n) == container_body |
As is the case of the forall
keyword, the parameters are allowed to depend on each other in an
arbitrary order, although cyclic dependencies are not allowed. The
parameters may either be types (in which case their types are
categories; see below) or ordinary values.
For instance, we may define complex numbers using
class Complex (R: Ring) == {
re: R;
im: R;
constructor complex (x: R) == { re == x; im == 0; }
constructor complex (x: R, y: R) == { re == x; im == y; }
} |
Notice that the user must specify a type for the parameter R. In this case, we require R to be a ring, which means that the ring
operations should be defined in R.
Here Ring is actually
an example of a category (see the chapter on categories for
more details), which might have been as follows:
category Ring == {
convert: Int -> This;
prefix -: This -> This;
infix +: (This, This) -> This;
infix -: (This, This) -> This;
infix *: (This, This) -> This;
} |
6.User defined
converters
When introducing new classes, one often wants to define converters
between the new class and existing classes. For instance, given the
above container Complex
R, it is natural to define a converter from R to Complex R. Depending on the desired
transitivity properties of converters, there are three
important types of converters: ordinary converters, upgraders and
downgraders. We also recall that appropriate mappers defined using the
map construct automatically induce converters (see the section
about the map construct).
6.1.Ordinary converters
Ordinary converters admit no special transitivity properties. They are
defined using the special identifier convert and usually correspond to casts. A typical such converter
would be the cast of a double precision number of type Double to an arbitrary precision number
of type Floating and
vice versa:
convert: Double -> Floating;
convert: Floating -> Double; |
6.2.Upgraders
Upgraders usually correspond to constructors. For instance, with the
example of the container Complex
R in mind, it is natural to define a converter from
any ring R to Complex R by
forall (R: Ring) upgrade (x: R): Complex R == complex x; |
This definition is equivalent to
forall (R: Ring) convert (x :> R): Complex R == complex x; |
In other words, upgraders are left transitive: whenever we have a type
T with a converter from
T to R, then the upgrader also defines a
converter from T to Complex R. For instance, we
automatically obtain a converter from Integer
to Complex Rational.
6.3.Downgraders
In contrast to upgraders, downgraders are right transitive.
Downgraders correspond to type inheritance in other languages such as
C++, but with the big advantage that the inheritance is abstract, and
not related to the internal representation of data. For instance, with
the example class Point
from the beginning of this section and some reasonable implementation
of a class Color in
mind, consider the class
class Colored_Point == {
p: Point;
c: Color;
constructor colored_point (p2: Point, c2: Color) == {
p == p2;
c == c2;
}
} |
Then the method .postfix
p provides us with a downgrader from Colored_Point to Point:
downgrade (cp: Colored_Point): Point == cp.p; |
Notice that this definition is equivalent to
convert (cp: Colored_Point) :> Point == cp.p; |
Given any converter from Point
to another type T, the
downgrader automatically provides us with a converter from Colored_Point to T.
For instance, given the converter
convert (p: Point): Vector Double == [ p.x, p.y ]; |
we automatically obtain a converter from Colored_Point
to Vector Double.
7.Flattening
In Mathemagix, instead of implementing pretty
printing functions for new user defined classes, we rather defining
flattening functions, which compute syntactic representations for
instances of the new classes. More precisely, given a user defined
class T, the user can
define a function
Mathemagix implements a default pretty printer
for Expressions of type Syntactic.
In fact, any Mathemagix type T comes with such a flattening function.
In particular, a default implementation is provided automatically when
declaring a new class, but the default function can be overridden by
the user. For instance, with the container Complex
R as before, we may define a flattener for complex
numbers by
forall (R: Ring)
flatten (z: Complex R): Syntactic ==
flatten (z.re) + flatten (z.im) * syntactic ('mathi); |
Here 'mathi
stands for the standard name for the mathematical constant  , and addition and multiplication of syntactic
expressions are provided by basix/syntactic.mmx. The
advantage of using the flattening mechanism is that Mathemagix
takes care of some elementary simplifications when printing syntactic
expressions. For instance, the complex number
, and addition and multiplication of syntactic
expressions are provided by basix/syntactic.mmx. The
advantage of using the flattening mechanism is that Mathemagix
takes care of some elementary simplifications when printing syntactic
expressions. For instance, the complex number  will be printed as expected and not as something similar to
will be printed as expected and not as something similar to  .
.
© 2012 Joris van der Hoeven
Permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU General Public License. If you
don't have this file, write to the Free Software Foundation, Inc., 59
Temple Place - Suite 330, Boston, MA 02111-1307, USA.
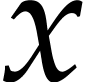 and
and 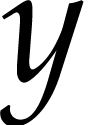 coordinates might be defined as follows:
coordinates might be defined as follows:
 , and addition and multiplication of syntactic
expressions are provided by basix/syntactic.mmx. The
advantage of using the flattening mechanism is that
, and addition and multiplication of syntactic
expressions are provided by basix/syntactic.mmx. The
advantage of using the flattening mechanism is that  will be printed as expected and not as something similar to
will be printed as expected and not as something similar to  .
.