| Declarations and control structures |
1.Declaration and
scope of variables
Constants are defined using the keyword ==:
welcome: String == "Welcome to Mathemagix!";
ok? : Boolean == sunny? and warm?; |
Mutable variables can be defined and modified
using the keyword :=, as in the following example:
i: Int := 1;
while i <= 10 step i := i + 1 do
mmout << 10 << " * " << i << " = " << 10 * i << lf; |
The skope of a variable corresponds to the innermost block
delimited by { and }
in which the variable is defined. For instance:
i: Int == 1;
if cond? then {
i: Int == 2;
foo (i, i);
}
mmout << i << lf; // i contains 1 at this point |
Global variables admit the entire file as their skope. More
complex scoping rules which apply in the case of multiple file
projects or in presence of modules will be discussed in the chapter about programming in the large.
Regular identifiers should match the regular
expression [a-zA-Z_]+[a-zA-Z0-9_$?]*. That is, the
names of constants, variables, function names, macros and types should
-
only contain letters, digits and the special characters _,
$ and ? ; and
-
start with a letter or _ or $.
In addition, it is customary to use lowercase identifiers for
constants, variables and functions, and to capitalize the first letter
of each word in identifiers for types (e.g. Integer or Sparse_Vector).
Moreover, identifiers for boolean variables and predicates are usually
suffixed by ?.
Besides regular identifiers, Mathemagix supports
various special identifiers, such as infix
+ for addition. These will be discussed in more
detail in the section about identifiers.
2.Declaration of
simple functions
The declaration of functions will be discussed in more detail in the
chapter about functions. Simple function declarations admit the
following syntax:
function_name (arg_1: Type_1, …, arg_n: Type_n): Ret_Type == body; |
For instance:
cube (n: Int): Int == n*n*n; |
It should be noticed that this declaration is actually equivalent to
the following declaration of cube as a “function
constant”:
cube: Int -> Int == (n: Int) :-> (n*n*n: Int); |
As in the case of ordinary variables, functions can be mutable:
foo (n: Int): Int := n*n;
foo := (n: Int) :-> (n*n*n: Int); |
The return
statement can be used to exit the function with a given return value.
For instance:
search_index (item: Int, v: Vector Int): Int == {
for i: Int in 0..#v do
if v[i] = item then return i;
return -1;
} |
3.Macros
Mathemagix provides the keyword ==> for the declaration of
macros. Since names of types can sometimes be rather long, macros are
often used in order to abbreviate them. For instance:
POL ==> Polynomial Rational;
p: POL == polynomial (1, 2, 3); |
Since such abbreviations are usually local to a file, it is customary
to declare all macros at the start of the file and to use the private keyword
in order to keep them private to the file. For instance:
include "numerix/rational.mmx";
include "algebrabix/polynomial.mmx";
include "algebrabix/matrix.mmx";
private {
POL ==> Polynomial Rational;
MAT ==> Matrix Rational;
}
// new routines on rational polynomials and matrices |
It is also customary to capitalize all letters in names of macros.
Remark 1. Macros with
arguments are not yet supported by the compiler, but planned.
4.Conditional statements
Conditional statements are of one of following two forms
if condition? then then_body
if condition? then then_body else else_body |
The bodies of the then-part and the else-part can either be single
instructions or blocks of instructions braced into {…}. For instance, we may write
if done? then {
clean_up ();
return;
} |
fib (n: Int): Int == {
if i <= 1 then return 1;
else return fib (n-1) + fib (n-2);
} |
Notice that the if-then-else construct can also be used as an
expression:
mmout << "Take a " << (if warm? then "shirt" else "jacket") << lf; |
5.Simple pattern matching
It often occurs that a list of actions has to be undertaken depending
on the value of some expression. This kind dispatching can be achieved
using the match instruction which has the syntax
match expression with match_body |
where match_body is a sequence of cases of the
following form:
case case_pattern do case_body |
For instance:
fib (n: Int): Int ==
match n with {
case 0 do return 1;
case 1 do return 1;
case _ do return fib (n-1) + fib (n-2);
} |
This is a simple example of the general mechanism of pattern matching,
which will be discussed in more details in the chapter
about abstract data types.
6.Loops
Loops are constructed as follows:
loop_modulator_1 … loop_modulator_n do loop_body |
where the loop modulators are among one of the following five types:
for variable: T in values
for instruction
while condition?
until contition?
step instruction |
A simple example of how to use the for-in modular is the
following:
for i: Int in 1 to 10 do
mmout << i << " * " 10 << " = " << i * 10 << lf; |
The expression 1 to 10
is an example of a “generator”. For more information on
such objects, we refer to the section on
generators. The for-in loop is equivalent to
the following one which uses the for,
while and step modulators:
for i: Int := 1 while i <= 10 step i := i + 1 do
mmout << i << " * " 10 << " = " << i * 10 << lf; |
The for modulator
(without in) is really
syntactic sugar: the above code is essentially the same as
i: Int := 1;
while i <= 10 step i := i + 1 do
mmout << i << " * " 10 << " = " << i * 10 << lf; |
except that the scope of the variable i
is bound to the body of the loop when using the for modulator. Similarly, the step modulator could have been moved to
the body of the loop:
for i: Int := 1 while i <= 10 do {
mmout << i << " * " 10 << " = " << i * 10 << lf;
i := i + 1;
} |
However, this way of writing things is slightly longer and less
readable. Furthermore, this kind of rewriting becomes less
straightforward in presence of continue
instructions (see below).
The condition of the while
modulator is tested each time before executing the body of the loop.
By contrast, the condition of the until
modulor is tested only at the end of the loop. For instance, in the
following loop, the body is executed at least one time:
until i > 10 do {
mmout << "i= " << i << lf;
i := i + 1;
} |
It should also be noticed that modulators of the same type can very
well be used several times. For instance, the following loop will
output the numbers  ,
, 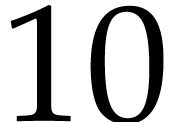 and
and 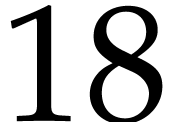 :
:
v1: Vector Int == [1, 2, 3];
v2: Vector Int == [4, 5, 6];
for x1: Int in v1
for x2: Int in v2 do
mmout << x1 * x2 << lf; |
In this last example, even though v1
and v2 are not of type
Generator Int, there
exists a prefix operator @
from Vector Int to Generator Int which allow
us to write for x1: Int in
v1 and for x2: Int in
v2.
7.Loop interruption
and continuation
The execution of a loop can be interrupted using the break instruction. As soon as
a break instruction is
encountered, execution will resume at the end of the loop. For
instance, the following loop will only output the numbers one until
five:
for i: Int in 1 to 10 do {
if i = 6 then break;
mmout << i << lf;
} |
In a similar way, the continue instruction interrupts the execution of the body of the loop,
but continues with the execution of the next cycle. For instance, the
following code will display all numbers from one to ten, except for
the number six:
for i: Int in 1 to 10 do {
if i = 6 then continue;
mmout << i << lf;
} |
8.Exceptions
Exceptions in Mathemagix are handled using a
conventional try-catch mechanism. This mechanism resides on three
keywords:
-
The “raise
exception” instruction with one
argument exception
of an arbitrary type T
is used in order to raise an exception of type T.
-
The “try
try_body” instruction protects
the block try_body of instructions against
exceptions, by allowing the user to provide exceptions handlers
for exceptions of various types.
-
Any number of “catch
(exception: T) catch_T_body”
instructions can occur at the end of the try_body.
Whenever an exception of type T
occurs, it is handled by the corresponding exception handler catch_T_body.
Exceptions which could not be catched are propagated further
outwards.
A typical example of a safe routine for printing values of a partially
defined function is
print_values (f: Double -> Double): Void == {
for x: Double in -5.0 to 5.0 do {
try {
y: Double == f x;
mmout << x << "\t" << y << lf;
catch (err: String) {
mmout << x << "\t" << err << lf;
}
}
}
} |
A typical example of a corresponding partially defined function is
foo (x: Double): Double == {
if x <= -2.0 then return x + 2.0;
if x >= 2.0 then return x - 2.0;
raise "out of range";
} |
Applying print_values
on foo yields the
following output
-5 -3
-4 -2
-3 -1
-2 0
-1 out of range
0 out of range
1 out of range
2 0
3 1
4 2
5 3
Standard Mathemagix libraries usually raise
errors of the type Exception instead of String.
For this reason, one might wish to replace the type of err by Exception.
In that case the routine foo
should be replaced by
foo (x: Double): Double == {
if x <= -2.0 then return x + 2.0;
if x >= 2.0 then return x - 2.0;
raise exception ("out of range", x);
} |
The second argument of exception allows the user to specify a reason for the exception, such
as an offending value or a line in the source code which triggered the
exception.
9.Comments
Mathemagix supports two types of comments. Short
comments start with // and extend to the end of the physical line:
class Complex (R: Ring) {
re: R; // real part of the complex number
im: R; // imaginary part of the complex number
…
} |
Long multi-line comments should be braced into /{ …
}/ and can be nested:
y == hacked_function x; /{ FIXME:
This is a dangerous hack /{ which occurs only on the first of april }/
A skilled extraterrestian should be able to fix it
}/ |
© 2012 Joris van der Hoeven
Permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU General Public License. If you
don't have this file, write to the Free Software Foundation, Inc., 59
Temple Place - Suite 330, Boston, MA 02111-1307, USA.
 ,
, 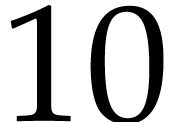 and
and 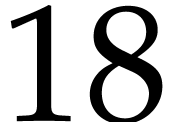 :
: