1.Original design goals

During the late ninetees, our wish for a new general purpose computer algebra language was motivated by two main reasons: the quasi-absense of free computer algebra systems and the non-existence of sufficiently general compiled computer algebra languages. At that time, there were very few free computer algebra systems around. The systems Axiom, Maxima and Reduce, which are all free nowadays, carried proprietary licences by then. I found the Axiom system and its successor Aldor especially inspiring, and I originally intended to write something close to these.

Concrete plans for the Mathemagix project started in 1998, around the same time as the development of TeXmacs, which was originally intended as the interface for Mathemagix. Our original design goals were the following:

Strong typedness

Mathemagix should be strongly typed, with support for discrete and parameterized overloading, generic objects, compile-time type checking and, possibly, built-in support for expression types which interact with the type system.

High level control structures

Mathemagix should ultimately support high level control structures, like coroutines, generators, exceptions, continuations, etc. In the future we also wish to consider parallellism.

Runtime efficiency

This is a really a long-term goal, since writing a compiler is not a short-term objective. Nevertheless, the possibility to write a compiler which produces efficient code should be kept in mind. In particular, the language should support directives for controlling memory layout and inlining in a way which is naturally compatible with the type system.

Reusability of extern libraries

Before achieving runtime efficiency of Mathemagix itself, we aim to achieve runtime efficiency through the extensive reuse of existing dedicated libraries written in other languages. Mathemagix should therefore implement transparent mechanisms for reusing extern libraries and in particular C++ template libraries. Special care should be taken of garbage collection.

Good scalability

It should be possible to develop large computer algebra systems using Mathemagix in a natural and modular way. Special attention should be paid to constructs for programming in the large and the type system should naturally allow extensions of types and code.

2.History of the implementations

Since I had only one or two months every year to spend on the development of Mathemagix, I have hesitated a lot about the most efficient way to have “at least something working” in which I could test some of my mathematical algorithms, possibly written in C or C++. One important, but rather unrealistic, development goal was to be able to improve the system gradually, and implement the harder aspects of the type system in an incremental way.

My first failed attempt to directly write a compiler occurred between 1999 and 2002. I directly intended to integrate support for continuations, which made debugging quite complex, and the overall project too hard to be realistic with little development time available.

For my second attempt, which started in 2003, I decided to start with the implementation of an interpreter, with the additional requirement that it should be very easy to integrate existing C++ libraries, and in particular some of my own libraries for relaxed power series and computable real numbers. This new interpreter was called mmx-shell and came with a uniform typed extension facility mmx-extend for gluing external C++ libraries. In parallel, we started the development of a standard C++ library Mmxlib.

At the start of the ANR Gecko project in 2005, the new interpreter was severely reorganized into the interpreter mmx-light. The aim was to reach a far more modular design, such that Mathemagix would become a bunch of separate package, with possible interdependencies, and a standardized way to compile and install packages (based on Autotools). In particular, the interpreter and the glue were designed to be as independent as possible, making it a priori possible to use the glue for another language with a completely different syntax. In retrospect, this has been somewhat of a waste of time, but I have always been playing with the thought of deriving a Scheme implementation from Mathemagix, so that we might also use it as an extension language for TeXmacs.

However, the ultimate type system of Mathemagix is hard to implement in a dynamically typed interpreter. Indeed, expressions can be essentially overloaded, and, contrary to C++, the correct unambiguous type of an expression can not necessarily be determined at the level of the parent of the expression (e.g. when using it as an argument to a function call). Instead of endlessly hacking an inperfect interpreter, I therefore restarted the implementation of the current mmc compiler around 2007. The new compiler was directly written in Mathemagix itself, using the existing interpreter, and I rather quickly managed to produce a compiler which could compile itself. The possibility to declare functions inside functions and easily construct expressions and vectors turned out to be a huge accelating factor.

At the time of writing (november 2012), the compiler mmc has reached a quite stable status which makes it possible to write non trivial projects with it. In the meantime, Grégoire Lecerf has developed the interpreter mmi, which is just another backend for the compiler. Besides the compiler itself, the automagix, caas, mcoq and mmail packages can be compiled using mmc. In the near future, we intend to experiment writing packages which rely more heavily on the support of categories and templates.

However, some parts of the implementation of mmc have become a bit hacky, so it is time for a partial rewrite at least. In the future, we intend to build a robust API for typed disambiguous programs which are manipulated a lot inside the compiler. After this reorganization, it should be easier to write a high quality optimizer. We also intend to replace the C++ backend by a C backend and mmi by a backend with JIT support.

Another point which remains quite puzzling is to have some support for untyped expressions, whether this support exists directly in the compiler, or in a separate system. Indeed, a typical end user of a computer algebra system may want to compute in a shell without specifying the types of 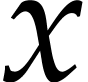and 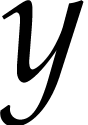, or define the cube function simply by cube(x) == x*x*x. In 2012, we therefore started the developement of a new library for symbolic computation named caas. This library comes with a new untyped interpreter, but with a language which is similar to the official language recognized by the compiler. Future investigations will learn us how well the untyped and the typed view of the world can be integrated. One other main reason behind caas is that it could become a reasonable replacement for mmx-light, and a suitable light weight front-end for use in education.

3.History of the type system

A first draft for the type system was developed during this period (199*), largely inspired by Axiom and Aldor.

A first major change in the language occurred in 2001, after a discussion with Dan Grayson. He convinced me that the Axiom/Aldor way to import modules is suboptimal, since it requires the user to do a lot of bookkeeping of when to import what. Also, an often heard complaint about the Axiom system was that the hierarchy of categories is rather rigid.

For these reasons, I decided to introduce the forall construct in Mathemagix. At that point, I realized that it would be a good idea to associate explicit types to ambiguous expressions. The main task of the compiler would thus be to transform “ambiguously typed expressions” into “unambiguously typed expressions”. I later realized that this point of view is very close to the “système F”, introduced by Girard. However, the design of a compiler which performs the above disambiguization was (and partly still remains) a non trivial challenge.

Moreover, in early versions of the language, I also wanted support for implicit type conversions. It turned out that this requirement really introduced too many sources of ambiguity into the language, which made it really hard to design a comprehensive set of rules and primitives for which interpretations to prefer over which other interpretations. In 2011, we therefore decided to remove implicit conversions from the language, which made it possible to greatly simplify the compiler. For similar reasons, Stephen Watt decided to remove implementations from Axiom in is implementation of the Aldor language.

It should be noticed that, in the case of Mathemagix, removal of implicit conversions was is not a big sacrifice. Based on the forall primitive, an acceptable substitute was found, which essentially obliges the programmer to specify which arguments to functions accept implicit conversions. This is cleaner anyway, in our model where all declarations should be typed very precisely.

Notice that a sketch of the type system of Mathemagix can be found in my paper Overview of the Mathemagix type system.