| Unions and free data types |
1.Introductory example
Mathemagix classes provide a simple way to
introduce new data types with specified data fields, methods,
constructors and an optional destructor. Mathemagix
unions provide a convenient tool for the definition of unions and more
general free data types.
One typical example of a union is the type of finite integer
sequences, defined as follows:
union Sequence == {
null ();
cons (head: Integer, tail: Sequence);
} |
Any such sequence is a formal expression of the form
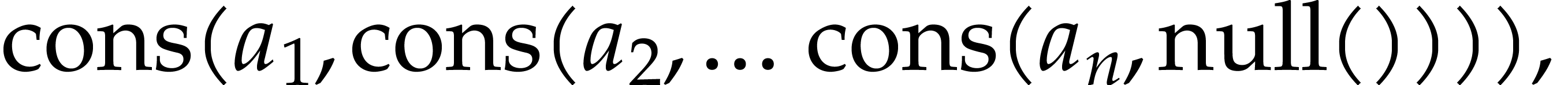
where  are integers. The symbols null and cons
are called the constructors for the union and any union of
the type Sequence is
always either of the form null
() or cons (h,
t), with h:
Integer and t:
Sequence. The declaration of the union Sequence automatically gives rise to
predicates
are integers. The symbols null and cons
are called the constructors for the union and any union of
the type Sequence is
always either of the form null
() or cons (h,
t), with h:
Integer and t:
Sequence. The declaration of the union Sequence automatically gives rise to
predicates
null?: Sequence -> Boolean;
cons?: Sequence -> Boolean; |
which allow the user to determine the kind of union. The symbols head and tail induce partially defined
accessors
postfix .head: Sequence -> Integer;
postfix .tail: Sequence -> Sequence; |
If a union s: Sequence
is of the form cons (h,
t), then cons?
s holds and we may obtain h
and t via the
expressions s.head and
s.tail respectively.
For instance, the following function can be used in order to compute
the length of a sequence:
prefix # (s: Sequence): Int ==
if null? s then 0 else #s.tail + 1; |
Pattern matching provides us with an alternative way to do this:
prefix # (s: Sequence): Int ==
match s with {
case null () do return 0;
case cons (_, t: Sequence) do return #t + 1;
} |
Mathemagix also provides the following syntax
for doing the same thing:
prefix # (s: Sequence): Int == 0;
prefix # (cons (_, t: Sequence)): Int == #t + 1; |
Notice that this syntax relies on the mechanism of conditional
overloading (see the section on conditional
overloading).
Likewise classes, unions can be parameterized. The List T container is a typical example of
a parameterized union which generalizes the union Sequence:
union List (T: Type) == {
null ();
cons (head: T, tail: List T);
} |
2.Structures
The general syntax for the declaration of a union is the following:
union S == {
cons_1 (field_11: T_11, …, field_1n1: T_1n1);
…
cons_k (field_k1: T_k1, …, field_knk: T_knk);
} |
This declaration in particular induces the declaration of functions
cons_1: (T_11, …, T_1n1) -> S;
…
cons_k: (T_k1, …, T_knk) -> S; |
These functions cons_1,
 , cons_k
are called the constructors for S, and all instances of S are expressions which are
built up freely using these constructors. Hence, any instance x has the form cons_i (y_1, …, y_ni) for exactly
one index i and y_1: T_i1,
, cons_k
are called the constructors for S, and all instances of S are expressions which are
built up freely using these constructors. Hence, any instance x has the form cons_i (y_1, …, y_ni) for exactly
one index i and y_1: T_i1,  ,
y_ni: T_ini. The
declaration of S also
declares inspection predicates
,
y_ni: T_ini. The
declaration of S also
declares inspection predicates
cons_1?: S -> Boolean;
…
cons_k?: S -> Boolean; |
such that cons_i? x
holds if and only if x
is of the form cons_i (y_1, …,
y_ni). The declaration of S
finally induces the declaration of partially defined
accessors
postfix .field_11 : S -> T_11;
… …
postfix .field_knk: S -> T_knk; |
Whenever x: S is of the
form cons_i (y_1, …,
y_ni) then y_j
can be retrieved via the expression x.field_ij.
Whenever x is not of
this form, the expression x.field_ij
is undefined and may provoke an error or worse.
Parameterized unions are defined in a similar way as ordinary unions
using the syntax
union S (Param_1: C_1, …, Param_p: C_p) == {
cons_1 (field_11: T_11, …, field_1n1: T_1n1);
…
cons_k (field_k1: T_k1, …, field_knk: T_knk);
} |
Such declarations induce declarations of constructors, inspection
predicates and accessors in the same way as their unparameterized
homologues.
In additional to the constructors, inspection predicates and
accessors, declarations of (parameterized) unions also give rise to
the following additional functions and constants for more low level
introspection:
postfix .kind: S -> Int;
cons_1_kind?: Int -> Boolean;
…
cons_k_kind?: Int -> Boolean;
cons_1_kind: Int;
…
cons_k_kind: Int; |
If x is of the form cons_i (y_1, …,
y_iki), then x.kind
is just the integer i-1.
The predicate cons_i_kind?
just checks whether the input integer is equal to i-1, so that cons_i?
x holds if and only if cons_i_kind?
x.kind holds. Finally, cons_i_kind
is equal to the integer i-1.
3.Extensible
unions
Under some circumstances, it is useful to add additional constructors
to unions a posteriori.
For instance, assume that we are writing a compiler for some language
and that the expressions of the language are represented by a union.
It might be that someone else would like to define a language
extension but still use as much as possible the existing functions in
the compiler for all kinds of manipulations of expressions. The
simplest solution would then be to extend the expression type a
posteriori with some new constructors provided by the extended
language, modulo customization of existing functions on expressions
whenever necessary.
Another important example is the design of a flexible type for
symbolic expressions. Symbolic expression types are usually unions of
various basic expression types, such as literals, integers, function
applications, sums, products, etc. Whenever someone develops a library
for a new kind of mathematical objects, say differential operators,
then it is useful if these new objects can be seen as a new kind of
symbolic expressions.
In Mathemagix, extensible unions can be declared
using the syntax
union S := {
cons_1 (field_11: T_11, …, field_1n1: T_1n1);
…
cons_k (field_k1: T_k1, …, field_knk: T_knk);
} |
The only distinction with respect to the mechanism from the previous
section is that we are now allowed to further extend the union using
the following syntax:
union S += {
extra_1 (added_11: X_11, …, added_1n1: X_1n1);
…
extra_l (added_l1: X_l1, …, added_lnl: X_lnl);
} |
An arbitrary number of such extensions can be made after the initial
declaration of S and
these extensions may occur in different files (provided that the file
with the initial declaration is (directly or indirectly) included in
each of these files).
Whenever we extend a union in the above way the corresponding new
constructors, inspection predicates and accessors are automatically
defined. The lower level inspection routines are also automatically
extended, although the actual values of extra_1_kind,
 , extra_l_kind
now depend on the initialization order, and are therefore harder to
predict. Nevertheless, the set of all these kinds is always of the
form
, extra_l_kind
now depend on the initialization order, and are therefore harder to
predict. Nevertheless, the set of all these kinds is always of the
form 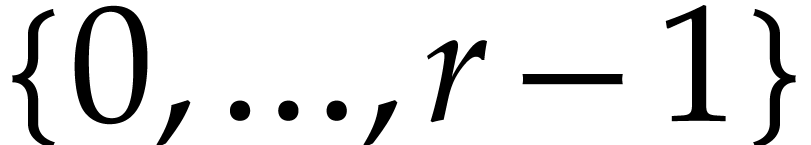 , where
, where  is the
total number of constructors.
is the
total number of constructors.
4.Pattern
matching
The constructors of a union can also be used as building bricks for so
called patterns. For instance, given the union
union Sequence == {
null ();
cons (head: Integer, tail: Sequence);
} |
from the beginning of this section, the expression
cons (_, cons (_, tail_tail: Sequence)) |
is a pattern which corresponds to all sequences of length at least
two, and with an explicit name tail_tail
for the typed name of the tail of the tail of the sequence.
More generally, there are six kinds of patterns:
-
Structural patterns, of the form cons
(p_1, …, p_n) where cons is a constructor with arity n of some union, and
p_1,  , p_n
are other patterns.
, p_n
are other patterns.
-
User defined patterns, to be described in the next section.
-
Wildcards of the form var:
T, where var
is the name of a variable and T
a type.
-
Unnamed wildcards of the form _:
T, where T
is a type.
-
The unnamed and untyped wildcard _.
-
Ordinary expressions.
One may define a natural relation “matches” on expressions
and patterns, and if an expression matches a pattern, then there
exists a binding for the wildcards which realizes the match. For
instance, the expression cons (1, cons
(2, cons (3, null ())) is said to match the pattern
cons (_, cons (_, tail_tail:
Sequence)) for the binding tail_tail
 cons (3, null
()).
cons (3, null
()).
Patterns can be used as arguments of the case keyword inside bodies of the match keyword. Whenever the pattern after case
matches the expression after match,
the wildcards are bound using the bindings of the match, and can be
used inside the body of the case
statement. For instance, we may use the following function in order to
increase all terms of a sequence with an even index:
even_increase (s: Sequence): Sequence ==
match s with {
case cons (x: Integer, cons (y: Integer, t: Sequence)) do
return cons (x, cons (y+1, even_increase t));
case _ do
return s;
} |
Patterns can also be used as generalized arguments inside function
declarations. In that case, the declaration is considered as a special
kind of conditionally overloaded function declaration.
For instance, the declaration
prefix # (cons (_, t: Sequence)): Int == #t - 1; |
is equivalent to
prefix # (s: Sequence | cons? s): Int == {
t: Sequence == s.tail;
#t - 1;
} |
Again, the bindings of potential matches are used as values for the
wildcards, which become local variables inside the function body.
5.User defined
patterns
Besides the patterns which are induced by constructors of unions, new
patterns may be defined explicitly by the user. The syntax for pattern
declaration is as follows:
pattern pat_name (sub_1: T_1, …, sub_n: T_n): PT == pat_body |
where the body pat_body
consist of a finite number of cases of the form
case pat_case do {
sub_1 == expr_1;
…
sub_n == expr_n;
} |
where pat_case is a
pattern. Assuming this declaration of pat_name,
any patterns p_1,  , p_n
of types T_1,
, p_n
of types T_1,  , T_n give
rise to a pattern pat_name (p_1,
…, p_n) of type PT.
This pattern is matched if and only if one of the patterns pat_case in the various cases for pat_name is matched (with
all occurrences of sub_1,
, T_n give
rise to a pattern pat_name (p_1,
…, p_n) of type PT.
This pattern is matched if and only if one of the patterns pat_case in the various cases for pat_name is matched (with
all occurrences of sub_1,
 , sub_n
in pat_case replaced by
p_1,
, sub_n
in pat_case replaced by
p_1,  ,
p_n). In that case, we
privilege the first case which matches, and bind var_i to expr_i
whenever sub_i is of
the form var_i: T_i.
,
p_n). In that case, we
privilege the first case which matches, and bind var_i to expr_i
whenever sub_i is of
the form var_i: T_i.
In a similar way as for unions, replacing ==
by != or += in the declaration of the above
pattern allows for the declaration of an extensible pattern resp. an actual extension of it. The above
declaration of the pattern pat_name
also gives rise to a generalized inspection predicate
pat_name?: PT -> Boolean; |
and functions
postfix .sub_1: PT -> T_1;
…
postfix .sub_n: PT -> T_n; |
which behave in a similar way as accessors of unions.
For instance, for sequences 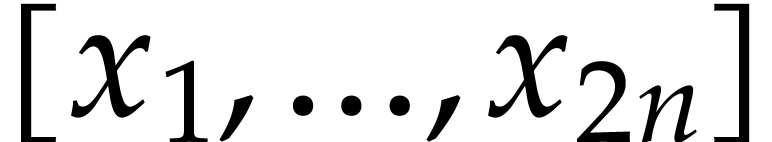 which really
represent association lists
which really
represent association lists 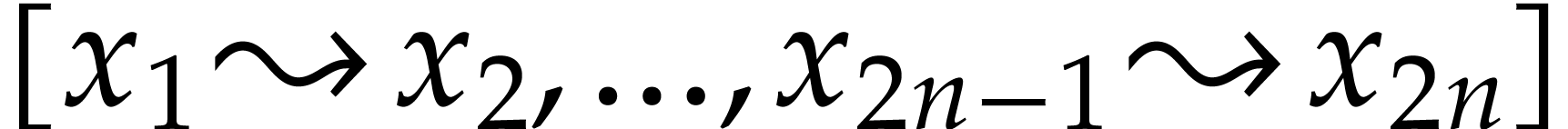 , we may use the
following pattern for retrieving the first association
, we may use the
following pattern for retrieving the first association  :
:
pattern assoc (key: Integer, val: Integer, next: Sequence): Sequence ==
case cons (k: Integer, cons (v: Integer, n: Sequence)) do {
key == k;
val == v;
next == n;
} |
The implementation of the predicate assoc?
is equivalent to
assoc? (s: Sequence): Boolean == cons? s and cons? s.next; |
and the implementations of the accessors postfix
.key, postfix
.val and postfix
.next are equivalent to
postfix .key (s: Sequence): Integer == s.head;
postfix .val (s: Sequence): Integer == s.tail.head;
postfix .next (s: Sequence): Sequence == s.tail.tail; |
6.Syntactic sugar for symbolic
expressions
As mentioned in the introduction of section ?, one
important special case where extensible unions are useful is for the
definition of a flexible type Symbolic
for symbolic expressions. This type is essentially a union type. For
instance, we might start with
union Symbolic := {
sym_undefined ();
sym_boolean (boolean: Boolean);
sym_literal (literal "literal": Literal);
sym_compound (compound: Compound);
} |
and further extend Symbolic
whenever necessary:
union Symbolic += {
sym_integer (integer: Integer);
} |
union Symbolic += {
sym_rational (rational: Rational);
} |
The prefix sym_
provides us with a clean syntatic distinction between a
“symbolic expression which contains an object of type T” and a mere object of type T. However, it would be
simpler to write integer?
instead of sym_integer?
as an inspection predicate, and it is somewhat cumbersome to implement
addition of symbolic integers using
infix + (sym_integer (i: Integer), sym_integer (j: Integer)): Symbolic ==
sym_integer (i + j); |
For this reason, Mathemagix provides us with a
special operator :: to be used for union constructors with one argument. For
instance, the constructor sym_integer would rather be
declared using
union Symbolic += {
sym_integer (integer :: Integer);
} |
This declaration automatically declares the synonym integer? for syn_integer?
and also introduces the simplified notation var
:: Integer for the pattern sym_integer
(var: Integer). Assuming the further implementation
of a constructor
convert (i: Integer): Symbolic == sym_integer i; |
we may then simplify the declaration of our addition on symbolic
integers into
infix + (i :: Integer, j :: Integer): Symbolic == i + j; |
In a similar way, Mathemagix provides support
for an operator ::> which allows us to mimick the notation :> used for a priori
conversions for their symbolic wrappers. This notation is best
illustrated with the example of an “symbolic converter from
symbolic integers to symbolic rational numbers”:
pattern sym_as_rational (as_rational ::> Rational): Symbolic := {
case sym_rational (x: Rational) do as_rational == x;
case sym_integer (x: Integer) do as_rational == x :> Rational;
} |
This allows us for instance to write
infix + (i :: Integer, x ::> Rational): Symbolic == i + x; |
7.Fast
dispatching
We already noticed that the mechanism of conditional overloading
induces a performance overhead (see the section on performance
issues concerning conditional overloading). In the case of
basic operations on symbolic expressions, such as additions, which are
overloaded dozens if not hundreds of times, this performance penalty
is too significant.
Fortunately, the union Symbolic
as described in the previous section is essentially an extensible
union type. Given a unary conditionally overloaded operation foo on symbolic
expressions, the appropriate routine to be called for a given input
x can often be
determined as a function of the integer x.kind
only. This makes it possible to use a fast lookup table instead of the
usual conditional overloading mechanism in this particular case. In
order to do so, we have to declare the operation foo using
foo (x: dispatch Symbolic): Symbolic := default_implementation |
Operations with higher arities and operations which involve other
types are treated in a similar way: the type of each argument involved
in the fast table lookup should be preceded by the keyword dispatch. For instance,
infix + (x: dispatch Symbolic, y: dispatch Symbolic): Symbolic := …;
postfix [] (x: dispatch Symbolic, i: Int): Symbolic := …; |
Notice that the size of the dispatch table is equal to the product of
the number of union constructors of all arguments on which we perform
our dispatching. For this reason, we do not allow dispatching on more
than two arguments.
Mathemagix also provides the keyword disjunction as a special case
of user defined patterns which is compatible with the above
dispatching mechanism. A typical example of a disjunction is
disjunction sym_scalar (scalar :: Scalar): Symbolic := {
sym_boolean _;
sym_integer _;
sym_rational _;
} |
© 2012 Joris van der Hoeven
Permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU General Public License. If you
don't have this file, write to the Free Software Foundation, Inc., 59
Temple Place - Suite 330, Boston, MA 02111-1307, USA.
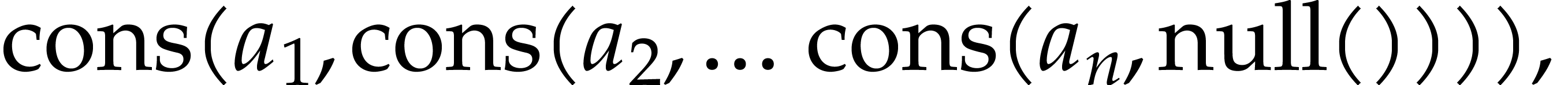
 are integers. The symbols
are integers. The symbols  ,
,  ,
,
 ,
, 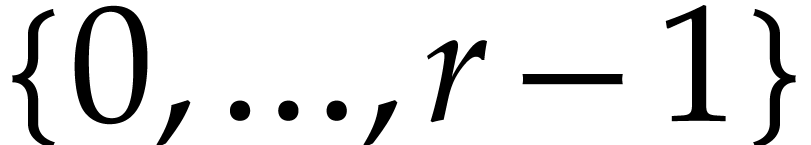 , where
, where 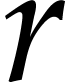 is the
total number of constructors.
is the
total number of constructors.
 ,
, 
 ,
,  ,
,  ,
,  ,
,
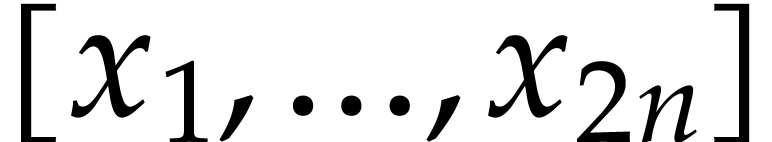 which really
represent association lists
which really
represent association lists 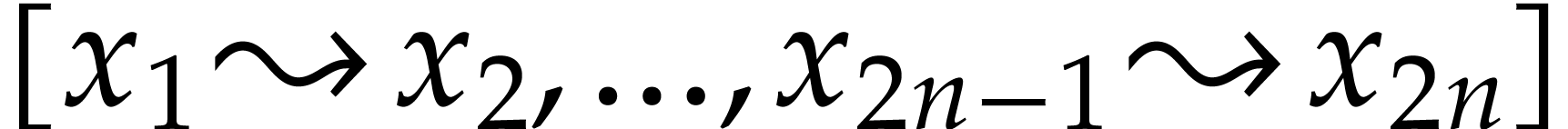 , we may use the
following pattern for retrieving the first association
, we may use the
following pattern for retrieving the first association  :
: