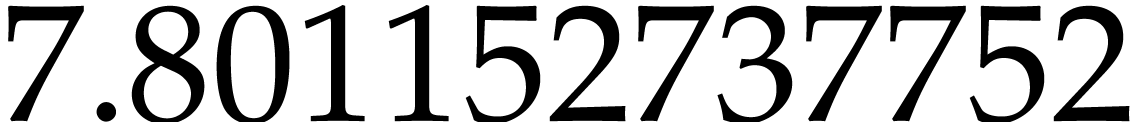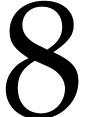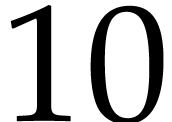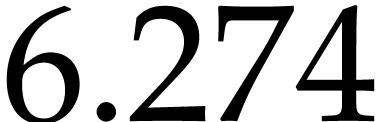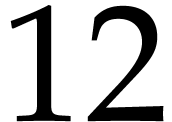1.Floatings

1.1.C++ interface

Floating point numbers of arbitrarily large size are available through the class floating defined in floating.hpp. This class is a simple wrapper to the class mpfr_t of the MPFR library.

#include<numerix/floating.hpp>
using namespace mmx;
void main () {
  floating<> a (2), b (3);
  mmout << a * b << "\n";
}

The precision can be set thanks to the global variable mmx_bit_precision.

Lower and upper certified approximates can be obtained as follows:

typedef rounding_helper<floating<> >::UV Up;
typedef rounding_helper<floating<> >::DV Down;
mmout << Up::sqrt (floating<> (2)) << "\n";
mmout << Down::sqrt (floating<> (2)) << "\n";

1.2.Mathemagix interface

The above floating type is glued to Mathemagix as Floating. Default bit-precision can be modified by setting the variable bit_precision.

Mmx]  

use "numerix";
type_mode? := true;

Mmx]  

a: Floating == 1.0

Mmx]  

exp a

Mmx]  

sin a

Mmx]  

1 / 0.0

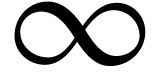Mmx]  

bit_precision := 128

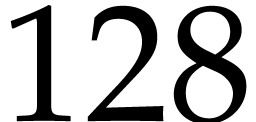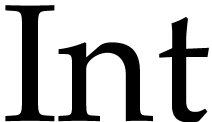
Mmx]  

exp 1.0

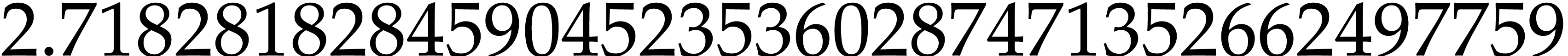2.Intervals

2.1.C++ interface

Interval are implemented within the class interval defined in interval.hpp.

#include<numerix/floating.hpp>
#include<numerix/interval.hpp>
using namespace mmx;
typedef interval<floating<> > Interval;
void main () {
  Interval a (2), b (3.0, 3.1);
  mmout << a * b << "\n";
}

2.2.Mathemagix interface

The above interval type is glued to Mathemagix as Interval. Classical scientific notation are used for pretty printing intervals.

Mmx]  

a == interval (0.999, 1)

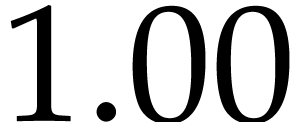Mmx]  

exp a

Mmx]  

radius a

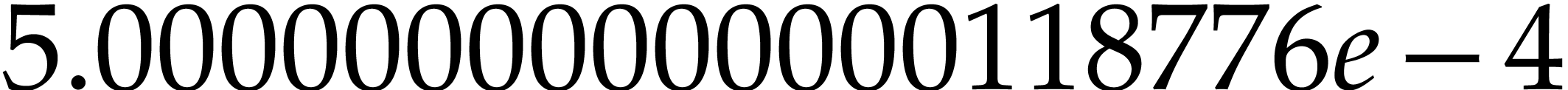Mmx]  

lower a

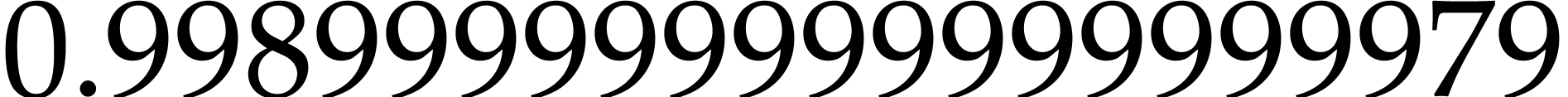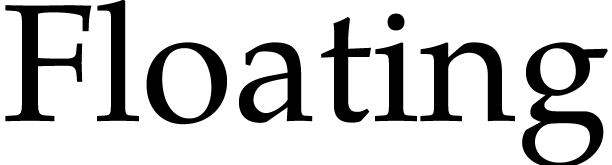
Mmx]  

upper a

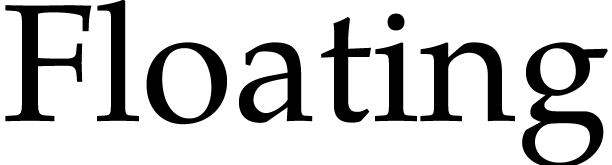
3.Complex numbers

3.1.C++ interface

Complex numbers are available through the class complex defined in complex.hpp. Over double one must include numerix/complex_double.hpp.

#include<numerix/complex_double.hpp>
using namespace mmx;
typedef complex<double> Complex;
void main () {
  Complex a (2), b (3.0, 0.1);
  mmout << a * b << "\n";
}

3.2.Mathemagix interface

The above complex type is glued to Mathemagix as Complex.

Mmx]  

I == complex (0, 1)

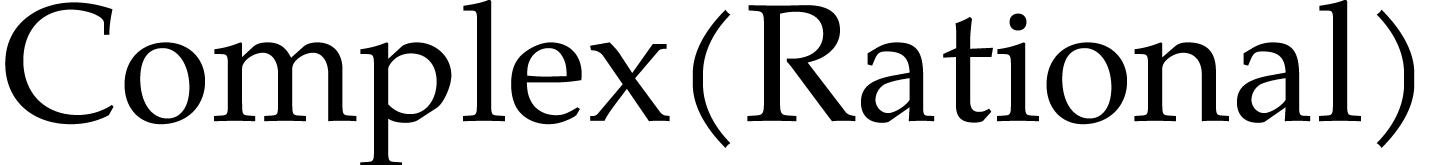
Mmx]  

I * I

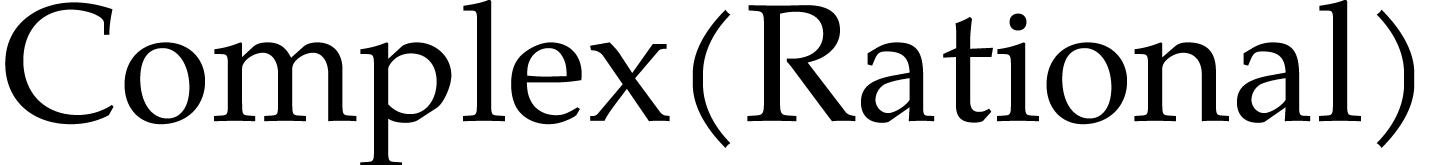
Mmx]  

1 / (1 + I)

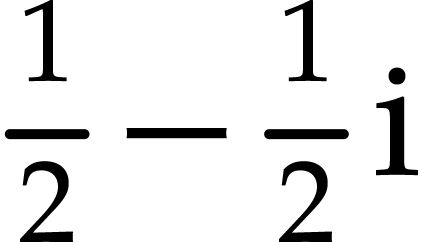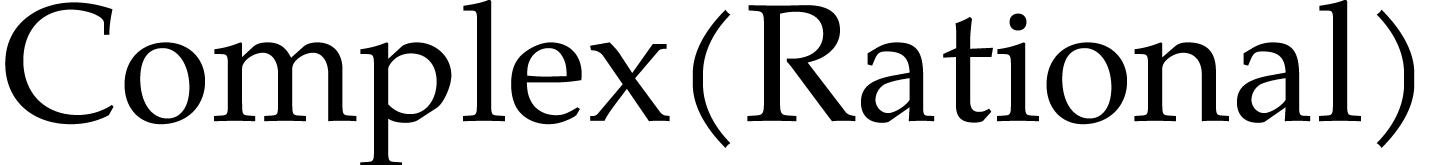
Mmx]  

I == complex (0 :> Floating, 1 :> Floating)

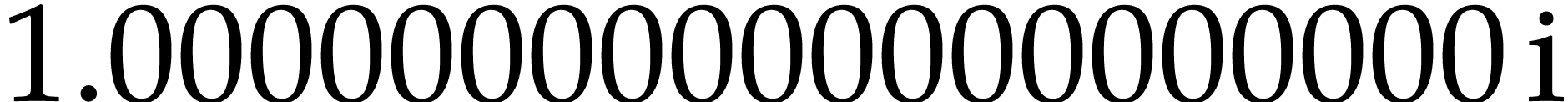Mmx]  

exp I

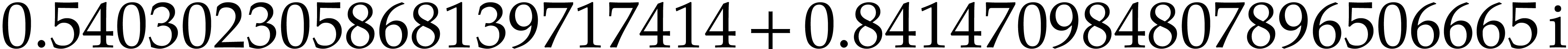4.Balls

4.1.C++ interface

Balls are implemented in the class ball defined in ball.hpp.

#include<numerix/ball.hpp>
using namespace mmx;
typedef ball<floating<> > Ball;
void main () {
  Ball a (2), b (3.0, 0.1);
  mmout << a * b << "\n";
}

4.2.Mathemagix interface

The above ball type is glued to Mathemagix as Ball.

Mmx]  

a : Ball (Floating, Floating) == ball (3.0, 0.1)

Mmx]  

[ center a, radius a ]

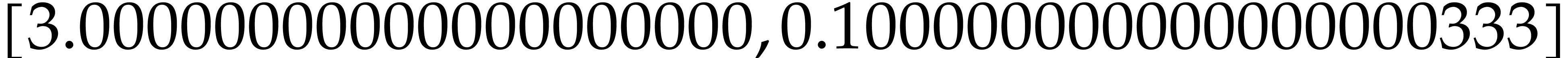
Mmx]  

M (n) ==
  if n = 0 then ball 2.0
  else if n = 1 then ball (-4.0)
  else 111 - 1130 / M (n-1) + 3000 / (M(n-1) * M(n-2));

Mmx]  

for n in 1 .. 15 do
  mmout << n << " " << M n << lf;