1.Identifiers
1.1.Regular identifiers
Identifiers are used as names for variables, functions, macros, types
and categories. Regular identifiers should match the regular
expression [a-zA-Z_]+[a-zA-Z0-9_$?]*. That is,
identifiers should
-
only contain letters, digits and the special characters _,
$ and ? ; and
-
start with a letter or _ or $.
In addition, it is customary to use the following guidelines when
choosing names:
-
Use lowercase names for variables and functions.
-
For names of types and categories, capitalize the first letter of
each word categories (e.g. Integer
or Ordered_Group).
-
Capitalize all letters in macro names.
-
Use the ? suffix
for names of predicates.
Besides the regular identifiers, Mathemagix
allows the programmer to use several types of special identifiers for the names of operators and special objects.
1.2.Operators
First of all, identifiers corresponding to the built-in operators (see
section ? below) are formed by prefixing them by one of
the keywords prefix, postfix,
infix and
operator.
For instance:
postfix ! (n: Int): Int == if n=0 then 1 else n * (n-1)!; |
Similarly, the instruction
mmout << map (infix *, [ 1, 2, 3 ], [ 4, 5, 6 ]) << lf; |
prints the vector  . The operator
. The operator
operator []: (t: Tuple T) -> Vector T; |
is used as a shorthand for the constructor of vectors (so that we may
write [ 1, 2, 3 ]
instead of vector (1, 2,
3)). Similarly, the operator postfix [] is used for accessing entries
of vectors and matrices.
Remark 1. TODO: in place
operators formed with the keyword inplace.
1.3.Named
access operators
In addition to the builtin operators, any regular identifier id can also be turned into
a postfix operator postfix
.id. For instance, when defining a class Point
by
class Point == {
x: Double;
y: Double;
constructor point (x2: Double, y2: Double) == {
x == x2;
y == y2;
}
} |
Mathemagix automatically creates two such
postfix operators for accessing the fields x
and y:
postfix .x: Point -> Double;
postfix .y: Point -> Double; |
Hence, we may define an addition on points using
infix + (p: Point, q: Point): Point ==
point (p.x + q.x, p.y + q.y); |
Additional operators similar to postfix
.x and postfix
.y can be defined outside the class
postfix .length (p: Point): Double ==
sqrt (square p.x + square p.y); |
Given a point p, we
then write p.length for
its length as a vector.
1.4.Other identifiers
The Mathemagix keywords, such as while, class,
etc. can also be turned into identifiers by prefixing
them with keyword.
Hence, keyword while
stands for the keyword while.
This notation is mainly using during formal manipulations of Mathemagix programs.
More generally, any valid string can be turned into an identifier by
putting it between quotes and prefixing it by the keyword literal. For instance, literal "sqrt" is
equivalent to the regular identifier sqrt,
literal "+"
is equivalent to the infix operator infix
+, and literal
"_+_" is an identifier which can only be
written using the keyword literal.
We finally notice that this is a special identifier which denotes the underlying instance
inside a class method.
2.Literal constants
Mathemagix provides three types of literal
constants: string literals, integer literals and floating literals. In
addition, there are several important constants, such as true and false,
which are really identifiers from the syntactic point of view.
2.1.Literal
strings
Short string constants are either written inside a pair of double
quotes "…":
mmout << "Hello world" << lf; |
Double quotes and backslashes inside strings should be escaped using
backslashes:
quote_char : String == "\"";
backslash_char: String == "\\"; |
Long string constants which avoid this kind of escaping can be formed
using the delimiters /"…"/, as
in the following example:
hello_world_example: String == /"
include "basix/fundamental.mmx";
mmout << "Hello world!" << lf;
"/
mmout << hello_world_example << lf; |
2.2.Literal
integers
An integer literal is a sequence of digits, possible preceded by a
minus sign. It matches the regular expression [-]?[0-9]+.
Examples are: 123456789123456789, -123.
The user should define a routine
literal_integer: Literal -> T; |
in order to allow literal integers to be interpreted as constants of
type T. The file basix/int.mmx of the standard library defines the routine
literal_integer: Literal -> Int; |
which allows literal integers to be interpreted as machine integer
constants. Arbitrary precision integers are supported by importing
literal_integer: Literal -> Integer; |
for numerix/integer.mmx.
2.3.Literal floating
point numbers
A literal floating point constant is a sequence of digits with a
decimal point inside, an optional sign and an optionalexponent. It
matches the regular expression
[-]?[0-9]+[.][0-9]+[[eE][-]?[0-9]+]?
The user should define a routine
literal_floating: Literal -> T; |
in order to allow literal floating poiunt numbers to be interpreted as
constants of type T. In
particular, the files basix/double.mmx and numerix/floating.mmx from the standard
library define the routines
literal_floating: Literal -> Double; // in basix/double.mmx
literal_floating: Literal -> Floating; // in numerix/floating.mmx |
For instance,
zero : Double == 0.0;
pi : Double == -3.14159;
funny: Floating == 1.2345679012345678901234567890e2012; |
Notice that 0. is not permited: one must write 0.0.
2.4.Special constants
Some constants are encountered so frequently, that it is useful to
mention them here, even though they are really identifiers from the
syntactic point of view:
-
The boolean constants false and true.
-
The standard input, output and error ports mmin, mmout and mmerr.
-
Several special control symbols for formatted output:
3.Operators
Table ? summarizes all standard Mathemagix
operators, together with their binding forces. For instance, the
expression
is naturally parsed as  . The operators can
roughly be divided into four groups:
. The operators can
roughly be divided into four groups:
-
Infix operators such as +
apply to one argument on the left and one argument on the right.
-
Prefix operators such as negation prefix
! apply to one argument on the right.
-
Postfix operators such as the factorial postfix
! apply to one argument on the left.
-
Other special operators, such as operator
[] for writing vectors [
1, 2, 3 ].
There are also some special postfix operators, such as function
application postfix ()
and named access operators such as postfix
.x (see section ?). Most operators are
infix operators, so infix notation is assumed to be the default,
unless stated otherwise. In the remainder of this section, we will
quickly survey the intended purpose of the various operators.
| Assignment operators |
==,
:=, +=, -=, *=,
/=, <<=, >>=, ==>, :=> |
| Function expressions |
lambda,
:-> |
| Input/output operators |
<<,
>>, <<<, >>>, <<*, <<% |
| Logical implication |
=>,
<=> |
| Logical disjunction |
or,
\/, xor |
| Logical conjunction |
and,
/\ |
| Relations |
=,
<, >, <=, >=,
!=, !<, !>, !<=,
!>=, :, in |
| Type conversion |
:>,
::, ::> |
| Arrows |
->,
~> |
| Ranges |
..,
to, downto |
| Addition and subtraction |
+,
-, @+, @- |
| Multiplication and division |
*,
/, @*, @/,
div, quo, rem, mod,
@, ><, %, & |
| Prefix operators |
!,
++, –, -, @-, @,
#, & |
| Operate on |
empty string |
| Power |
^ |
| Postfix operators |
++,
–, !, ', ‘,
~, #, (),
[] |
| Tuples and vectors |
(),
[] |
|
|
Table 1. Overview of all Mathemagix operators listed by increasing
binding force.
|
3.1.Assignment operators
The operators == and
:= are used for
declarations of constants and mutable variables, as described in the
sections about the declaration of variables and
functions. The operator ==>
is used for macro definitions (see the section about macro
declarations). The operator :=>
is reserved for future use.
The operator := can
always be used for the assignment of mutable variables. The operators
+=, -=, *=,
/=, <<= and >>=
are not yet exploited in the standard libraries, but there intended
use is “assignment of the left hand expression with the result
of the corresponding outplace operator applied to both
arguments”. For instance, the instruction
should considered to be equivalent to the assignment
Remark 2. As a future
extension of the compiler, we also intend to support assignment to
tuples, in order to assign several mutable variables at once. For
instance,
should swap the variables a
and b, and
should respectively increase a
and b with x and y.
3.2.Function
expressions
The special operators :->
and lambda are used for
writing functions directly as expressions. The expressions
(a_1: T_1, …, a_n: T_n) :-> (val: Ret_Type)
lambda (a_1: T_1, …, a_n: T_n): Ret_Type do val |
can both be used as a notation for the function with arguments a_1,  ,
a_n of types T_1,
,
a_n of types T_1,  , T_n, which returns the value val of type Ret_Type.
, T_n, which returns the value val of type Ret_Type.
3.3.Input/output operators
The operators <<
and >> are
respectively used for sending data to an output port and retrieving
data from an input port. The same notation is useful in analogous
circumstances, such as appending data to a vector or popping data from
a stack.
The operators <<<
and >>> are
used for sending and retrieving data in binary form. This allows for
instance for the implementation of efficient communication protocols
between different processes on the same or distant computers. The
operators <<* and
<<% are reserved
for future use.
Remark 3. Sometimes, we
also use the operators <<
and >> as shift
operators. For instance, given a power series f
in  , we might write f
<< n as a shorthand for the multiplication of
f with
, we might write f
<< n as a shorthand for the multiplication of
f with  .
However, it should be noticed that the binding force of << and >>
is not really appropriate for this type of use (a binding force
similar to the one of multiplication would be better for this kind of
use), so one carefully has to put brackets whereever necessary in this
case. In future versions of Mathemagix, this
kind of overuse of notations might be discouraged.
.
However, it should be noticed that the binding force of << and >>
is not really appropriate for this type of use (a binding force
similar to the one of multiplication would be better for this kind of
use), so one carefully has to put brackets whereever necessary in this
case. In future versions of Mathemagix, this
kind of overuse of notations might be discouraged.
3.4.Logical
operators
The operators =>,
<=>, \/, /\
stand for the standard logical connectors  ,
,
 ,
,  and
and  .
The prefix operator prefix
! stands for logical negation
.
The prefix operator prefix
! stands for logical negation  .
These operators are functions which can be redefined by the user, so
both arguments are evaluated in case of the logical connectors.
.
These operators are functions which can be redefined by the user, so
both arguments are evaluated in case of the logical connectors.
Mathemagix also provides the built-in operators
or and and which must take arguments of type Boolean. Moreover the
second argument of or
is evaluated only if the first argument evaluates to false. Similarly, the second argument of
and is evaluated only
if the first argument evaluates to true.
Remark 4. The operators
=>, <=>, \/,
/\ and ! can also be useful for bitwise
operations on numbers, even though the binding force is someone
inappropriate for this kind of use. One might also want to use /\ as a notation for
exterior products, again with an inappropriate binding force. In
future versions of Mathemagix, this kind of
overuse of notations might be discouraged.
3.5.Relations
The operators =, < , >, <=
and >= correspond to
the standard mathematical relations  ,
,  ,
,  ,
,  and
and
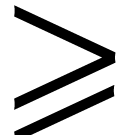 . When prefixing these relations with !, we obtain the operators
!=, !<, !>,
!<=, !>= which correspond to their
negations
. When prefixing these relations with !, we obtain the operators
!=, !<, !>,
!<=, !>= which correspond to their
negations  ,
,  ,
,  ,
,  and
and  .
.
In computational contexts, mathematical relations often admit a very
asymmetric nature: typically, it can be very easy to prove inequality,
but very hard to prove equality. It can even happen that we have an
algorithm for proving inequality, but no known algorithm for proving
equality. This is for instance the case for the class of so called
exp-log constants, constructed from the rational numbers using the
field operations, exponentiation and logarithm. In contexts where
equality testing is hard, it is therefore useful to make a notational
distinction between various types of equality, such as proven
equality, probable equality, syntactic equality, etc.
In Mathemagix, the intention of the notations
=, <, >,
<= and >= is that they stand for proven
relations. On the other hand, the negations !=,
!<, !>, !<=
and !>= are intended
to be mere shortcuts for their (not necessarily proven) negations.
Hence, a != b should
always be equivalent to !(a =
b). We are working on a comprehensive set of
additional relations for proven negations; they will probably be
denoted by =/, </, >/, <=/,
>=/. As an
additional rule, it is our intention that <=
(resp. >=)
is always equivalent to the disjunction of <
(resp. >)
and =. Thus a <= b should always be equivalent to
the statement a < b or a =
b.
The operator : should
be read “is of type”. For instance, x: T stands for “x is of type T”.
The operator in occurs
inside the for-in construct (see the
section about loops).
3.6.Type conversion
The operator :> can be used to convert an
expression of a given type into another, provided that an appropriate
converter was defined. More precisely, assume that expr has type S
and that we defined a converter convert:
S -> D. Then expr
:> D stands for the explicit conversion of expr into an expression of
type D. More
information about type conversions can be found in the section on
explicit type conversions and user
defined converters.
3.7.Arrows
The operator -> is
used as an efficient notation for function types, such as Int -> Int. One typical use case of
this notation is when a function is passed as an argument to another
function:
iterate (f: Int -> Int, n: Int) (k: Int) ==
if n = 0 then k else iterate (f, n-1) (f k); |
The operator ~> is
mainly used as a notation for key-value bindings whenever we
explicitly wish to create a table with given entries. For instance:
basic_colors: Table (String, Color) ==
table ("red" ~> rgb (1, 0, 0),
"green" ~> rgb (0, 1, 0),
"blue" ~> rgb (0, 0, 1),
"white" ~> rgb (1, 1, 1)); |
or
forall (T: Type)
invert (t: Table (T, T)): Table (T, T) ==
table (t[key] ~> key | key: T in t); |
3.8.Ranges
There are three standard kinds of range operators:
| start to
end |
|
Range from start
up to end
included |
| start ..
end |
|
Range from start
up to end not
included |
| start downto
end |
|
Range from start
down to end
included |
3.9.Arithmetic operations
The standard arithmetic operations +,
-, *, /
and ^ stand for
addition, subtraction, multiplication, division and powering. The @-prefixed variants @+, @-, @*,
@/ stand for  ,
,  ,
,  and
and
 . Notice that -
and @- can either be
infix or prefix operators.
. Notice that -
and @- can either be
infix or prefix operators.
Mathemagix provides the additional operators div, quo, rem
and mod for
division-related operations in rings which are not necessarily fields.
The operator div stands
for (usually partially defined) exact division. For instance, numerix/integer.mmx provides the operation
infix div: (Integer, Integer): Integer; |
but 5 div 3 is
undefined and might raise an error. The operators quo and rem
stand for quotient and remainder in euclidean domains. Hence, we
should always have

The operator mod stands
for modular reduction, so that the return type is usually different
from the source types. For instance 5 mod
3 would typically belong to Modular
(Int, 3) or Modular
(Integer, 3).
There are a few other operations with the same binding force as
multiplication. The append operator ><, also denoted by  , is typically used for appending strings, vectors and
table. For instance "a"
>< "b" yields "ab". The operator infix @ is used for functional
composition, whereas the operators %
and & are reserved
for future use.
, is typically used for appending strings, vectors and
table. For instance "a"
>< "b" yields "ab". The operator infix @ is used for functional
composition, whereas the operators %
and & are reserved
for future use.
3.10.Prefix
operators
The standard prefix operators in Mathemagix are
prefix ! (negation  ), prefix
++ (increment), prefix
– (decrement), prefix
- (unary
), prefix
++ (increment), prefix
– (decrement), prefix
- (unary  ), prefix @- (unary
), prefix @- (unary  ),
prefix @ (explode), prefix # (size), prefix & (reserved for future use).
),
prefix @ (explode), prefix # (size), prefix & (reserved for future use).
In addition, operator application of the form sin
x parses in a similar way as when sin behaves as a prefix operator. For
instance, sin cos x
should be parsed as  .
.
3.11.Postfix
operators
The standard postfix operators in Mathemagix are
postfix ++ (post
increment), postfix
– (post decrement), postfix
! (factorial  ), postfix ' (quote or derivative), postfix ‘ (unquote),
postfix ~ and postfix # (reserved for
future use).
), postfix ' (quote or derivative), postfix ‘ (unquote),
postfix ~ and postfix # (reserved for
future use).
++, –, !,
', ‘, ~,
#, (), []
In addition, Mathemagix provides the special
postfix operators postfix
() and postfix
[] for which we are allowed to put additional
arguments between the brackets. Hence, postfix
() stands for the traditional notation of function
application, whereas postfix
[] is typically used as an accessor
for compound data structures. Notice that f(g)(x)
is parsed as 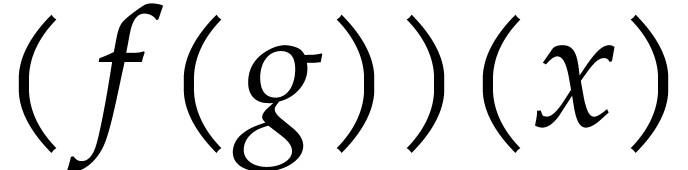 , whereas f
g x is parsed as
, whereas f
g x is parsed as  .
.
Using the operator postfix
(), we may generalize the classical notation for
function application to user defined types, such as vectors
of functions:
postfix () (v: Vector (Int -> Int), x: Int): Vector Int ==
[ f x | f: Int -> Int in v ]; |
3.12.Tuples
and vectors
The reserved special operator operator
() is used for building tuples of expressions (of
possibly different types), such as (1,
"hello"). The special operator operator [] is used as a notation for
explicit vectors, such as [ 1, 2, 3
], but it might be used for other purposes.
4.Generators
Generators are an elegant way for representing a stream of data of the
same type. For instance, the expression 1
to 10 of type Generator
Int allows us to write
for i: Int in 1 to 10 do
mmout << i << " * " << 7 << " = " << 7*i << lf; |
Mathemagix provides several constructs for
forming generators.
4.1.Range
generators
There are three standard kinds of range operators:
| start to
end |
|
Range from start
up to end
included |
| start ..
end |
|
Range from start
up to end not
included |
| start downto
end |
|
Range from start
down to end
included |
4.2.The explode operator
Many container types come with a prefix operator @ which returns a generator.
For instance, given a vector v
of type Vector T, the
expression @v has type
Generator T. Whenever
expr is an expression
such that @expr has
type Generator T, we
are still allowed to use expr
as the in-part of the
for-in construct. For instance:
for i: Int in [ 2, 3, 5, 7, 11, 13, 19 ] do
mmout << i*i << lf; |
4.3.The such that construct
One other important construct for forming generators is the
“such that” operator |. Given a generator g
of type Generator T,
the expression
(var: T in g | predicate? var) |
stands for the generator of all items in g
which satisfy the predicate predicate?.
For instance, consider the following naive implementation of the
predicate prime? which
checks whether a number is prime
prime? (n: Int): Boolean == {
for i: Int in 2..n do
if i rem i = 0 then return false;
return true;
} |
Then we may display the vector of all prime numbers below  using
using
mmout << [ p: Int in 1 to 1000 | prime? p ] << lf; |
Notice that this vector is constructed from the expression
(p: Int in 1 to 1000 | prime? p) |
of type Generator Int
using the bracket operator operator
[].
4.4.The where
construct
The vertical bar | can also be used as the “where” operator, using
the following syntax:
(expr var | var: T in g, predicate_1? var, …, predicate_n? var) |
Here g is again a
generator of type Generator
T, expr
var any expressions which involves var, and predicate_1?
var, …, predicate_n?
var an arbitrary number of predicates which involve
var. If expr var has type U, then the resulting expression has type
Generator U. For
instance,
mmout << [ i^2 | i: in 1 to 100 ] << lf; |
displays the vector of all squares of numbers from  to
to 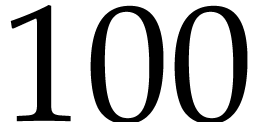 , and
, and
mmout << [ i^2 | i: in 1 to 1000, prime? (4*i + 3) ] |
displays the square of each number  such that
such that
 is prime.
is prime.
4.5.The where construct with multiple
generators
Mathemagix actually supports a generalization of
the where construct with multiple generators and predicates at the
right-hand side. This generalization is best illustrated with an
example:
mmout << [ p^i | p: Int in 1 to 1000, prime? p,
i: Int in 1 to 10, p^i < 1000 ] << lf; |
This code will print the unordered vector of all prime powers below
 .
.
4.6.Matrix
notation
A special where notation || is used for generators which allow to build rows of matrices
or similar two dimensional structures. Again, this notation is best
illustrated with an example. Assuming that the file algebramix/matrix.mmx
was included, the expression
[i+j | i: Int in 0 to 9 || j: Int in 0..10] |
computes the following matrix:

5.Mappers
Most Mathemagix containers implement a mapping
construct map.
This construct is used for applying one or more functions to all
entries of one or more containers.
Two simple examples for containers with a single parameter are
mmout << map (square, [ 1, 2; 3, 4 ]) << lf;
mmout << map (infix *, [ 1, 2, 3], [4, 5, 6]) << lf; |
These instruction respectively output the matrix  and the vector
and the vector  .
.
In the case of containers with more than one type parameter, one
usually has to provide one mapping function for every such parameter.
Consider for instance the following table:
t: Table (Int, String) == table (3 ~> "Hello", 4 ~> "Hi", 8 ~> "Bonjour"); |
Then the instruction
mmout << map (square, prefix #, t) << lf; |
prints the table  .
.
Syntactically speaking, the construct map
is an ordinary identifier. For instance, assuming that we defined a
container Complex R
(see the section on how to define your own
containers), a unary mapper for this container can be defined
as follows:
forall (R1: Ring, R2: Ring)
map (f: R1 -> R2, z: Complex R1): Complex R2 ==
complex (f z.re, f z.im); |
When providing your own containers, it is actually important to define
unary mappers of this kind, because such mappers automatically induce
converters between containers of the same kind
but with different type parameters. For instance, given a converter
from R1 to R2, the above mapper for complex numbers
automatically induces a converter from Complex
R1 to Complex
R2. This allows the user to write
z: Complex Rational == complex (1, 2); |
In general, such a converter is constructed whenever the user provides
a unary mapper which takes one mapping function for each parameter on
input together with a single container.
Remark 5. We notice that
the existence of a unary mapper is mandatory if a program both uses
the container in an generic and in a specialized way, and if
conversions between the generic and specialized versions of the
container indeed occur in the program. For instance, some mathematical
library lib.mmx might provide a generic function
forall (R: Ring)
conj (z: Complex R): Complex R == complex (z.re, -z.im); |
Now assume that we a client program client.mmx which
only works with complex numbers of type Complex
Double and which has specialized this type for
better performance. In memory, this means that such complex numbers
are represented by pairs of double precision numbers rather than pairs
of pointers to double precision numbers numbers as would be the case
for generic complex numbers. However, the routine conj from lib.mmx a
priori only applies to generic complex numbers, so conversions
between the specialized and the generic view are necessary if we want
to use this routine in client.mmx. As soon as the
required unary mapper is defined, these conversions are automatic.
© 2012 Joris van der Hoeven, Grégoire Lecerf
Permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU General Public License. If you
don't have this file, write to the Free Software Foundation, Inc., 59
Temple Place - Suite 330, Boston, MA 02111-1307, USA.
 . The operator
. The operator
 . The operators can
roughly be divided into four groups:
. The operators can
roughly be divided into four groups:
 ,
,
 ,
,  , we might write
, we might write  .
However, it should be noticed that the binding force of
.
However, it should be noticed that the binding force of  ,
,
 ,
,  and
and  .
The prefix operator
.
The prefix operator  .
These operators are functions which can be redefined by the user, so
both arguments are evaluated in case of the logical connectors.
.
These operators are functions which can be redefined by the user, so
both arguments are evaluated in case of the logical connectors.
 ,
,  ,
,  ,
,  and
and
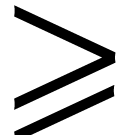 . When prefixing these relations with
. When prefixing these relations with  ,
,  ,
,  ,
,  and
and  .
.
 ,
,  ,
,  and
and
 . Notice that
. Notice that 
 , is typically used for appending strings, vectors and
table. For instance
, is typically used for appending strings, vectors and
table. For instance  ),
),  ),
),  ),
),
 .
.
 ),
), 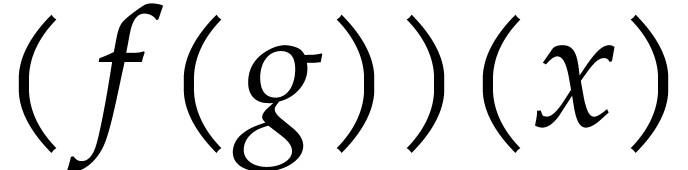 , whereas
, whereas  .
.
 using
using
 to
to 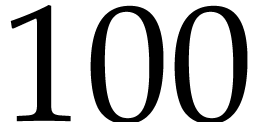 , and
, and
 such that
such that
 is prime.
is prime.
 .
.

 and the vector
and the vector  .
.
 .
.