| Functions |
1.Function declarations
1.1.Basic function declaration and application
The most basic form of a function declaration in
fun_name (arg_1: Type_1, …, arg_n: Type_n): Ret_Type == fun_body
The function name
|
We recall that
1.2.Tuple and generator arguments
Functions with an arbitrary number of arguments of a given type can be formed by using so called tuple types. More precisely, assume a function declaration of the form
|
Then the function 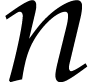 first arguments of types
first arguments of types 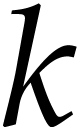 optional arguments which are all of type
optional arguments which are all of type
|
can be used to extract the vector of all entries with given indices from a given vector. Hence,
|
prints the vector 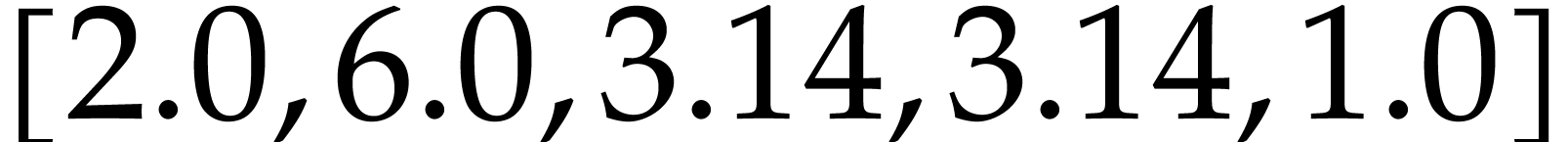 .
.
In a similar way, one may pass a generator instead of a tuple as a last argument of a function.
1.3.Recursive functions
Functions definitions are allowed to be recursive, such as the following routine for computing the factorial of an integer:
|
Functions which are defined in the same scope are also allowed to be
mutually recursive. An example of mutually recursive sequences are
Hofstadter's female and male sequences 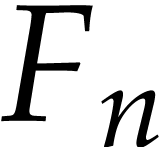 and
and
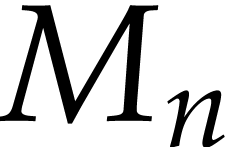 defined by
defined by 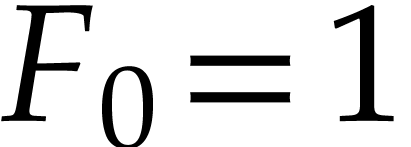 ,
, 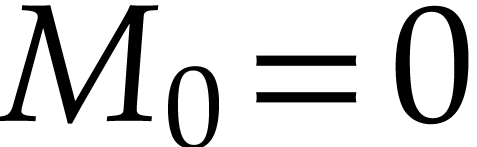 and
and
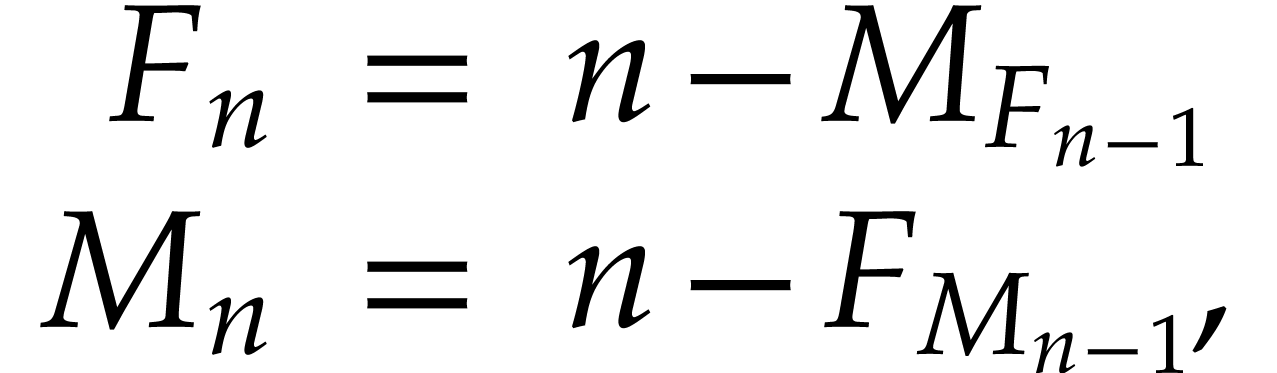
for  . They can be implemented in
. They can be implemented in
|
In large multiple file programs, it sometimes happens that the various mutually recursive functions are defined in different files, and thus in different scopes. In that case, prototypes of the mutually recursive functions should be defined in a file which is included by all files where the actual functions are defined. Protypes of functions are declared using the syntax
|
In case of the above example, we might define prototypes for
|
Next, a first file female.mmx would include common.mmx
and define
|
In a second file male.mmx, we again include common.mmx
and define
|
1.4.Dependent arguments and return values
Besides mutually recursive function definitions,
For instance, the following routine takes a ring together with an
element of this ring on input and displays the first 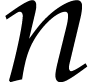 powers of this element:
powers of this element:
|
In this example, the type
The following code defines a container Fixed_Size_Vector
(T, n) for vectors with entries of type
|
The return type
2.Functional programming
Functions are first class objects in
2.1.Functions as arguments
A simple example of a function which takes a function predicate as an argument is
|
The 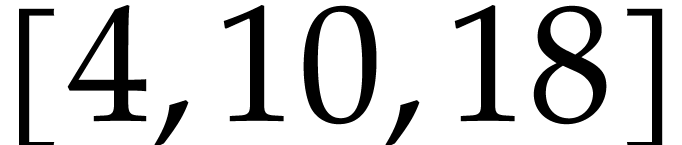 :
:
|
2.2.Functions as return values
A typical example of a function which returns another function is
|
This kind of functions are so common that
fun_name (arg_11: Type_11, …, arg_1n1: Type_1n1) … (arg_k1: Type_k1, …, arg_knk: Type_knk): Ret_Type == fun_body
This syntax allows to simplify the definition of
|
2.3.Functions as local variables
In a similar way that functions can be used as arguments or return values of other functions, it is possible to locally define functions inside other functions. One typical example is
|
Recursion and mutual recursion are still allowed for such local function declarations. For instance, we may generalize Hofstadter's example of female and male sequences by allowing the user to choose arbitrary initial conditions:
|
2.4.Mutable functions
As in the case of ordinary variables, functions can be declared to be mutable, using the syntax
fun_name (arg_1: Type_1, …, arg_n: Type_n): Ret_Type := fun_body
In that case, the function can be replaced by another function during the execution of the program:
|
In section ? below, we will how the mechanism of conditional overloading can exploit this possibility to dynamically replace functions by others.
3.Discrete overloading
In classical mathematics, operators such as  are heavily overloaded, in the sense that the same notation can be
used in order to add numbers, polynomials, matrices, and so on. One
important feature of
are heavily overloaded, in the sense that the same notation can be
used in order to add numbers, polynomials, matrices, and so on. One
important feature of
The simplest mechanism of discrete overloading allows the user to redefine the same symbol several times with different types. For instance,
|
In this case, the variable
|
Indeed, in the definition of
|
is ambiguous and will provoke an error message of the compiler. In
such cases, we may explicitly disambiguate
|
In case of doubt, successions of disambiguations, such as
Of course, overloading is most useful in the case of functions, and the mechanism described above applies in particular to this case. For instance, we may define
|
Then we may write
|
Overloaded functions can very well be applied to overloaded
expressions. For instance, the expression
|
It should also be noticed that both the arguments and the return
values of functions can be overloaded. For instance, we may overload
|
After this, the expression
4.Parametric overloading
4.1.The forall construct
Besides discrete overloading,
The general syntax for making one or more parametrically overloaded declarations is
|
The parameters
|
It states that for any type
|
In this case, any type 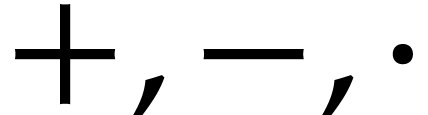 and a converter
and a converter
Assuming a context in which both the types
|
Although this is usually not necessary, it is sometimes useful to make
the values of the parameters explicit, for instance in order to make
expressions less ambiguous. This can be done using the
|
4.2.Grouping forall statements
It often happends that several generic routines share the same
parameters. In that case, they can be grouped together in a common  , assume that we are developing a
container
, assume that we are developing a
container 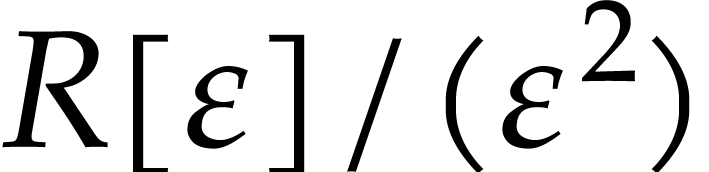 (see also the
section on container classes):
(see also the
section on container classes):
|
Then we may define a ring structure on
|
4.3.Additional assumptions on parameters
It often happens that template parameters need to fulfill several
requirements, such as being a ring and an ordering at the same time.
|
Such additional assumptions can naturally be included in
|
4.4.Partial specialization
It frequently occurs that for specific values of the template parameters, the generic implementation of the template can be further improved. For instance, consider the following generic implementation of a power operations on field elements:
|
This implementation uses binary powering and is more or less as
efficient as it can get for elements in a generic field. However, in
the “field”
|
In general, a first template (or function) is more particular than a
second one, if any possible type (i.e. by substituting
concrete values for the parameters) of the first template is also a
possible type of the second one. For instance, the first above
implementation of
It should be noticed that the relation “is more particular than” is only a partial ordering. For instance, none of the two following routines is more particular than the other one:
|
Applying the function
|
Indeed, this routine is more particular than each of the two generic
implementations of
It should be noticed that the relation “is more particular than” does not necessarily mean that some of the parameters have to be substituted by actual values in order to become “more particular”. For instance, consider the prototypes of two templates for the computation of determinants:
|
Then the second template is more particular than the first one, so it will be the preferred implementation when computing the determinant of a matrix with entries in a field.
5.Type conversions
5.1.Implicit conversions
In
|
we may use the expression
The operator
-
During the declaration of variables. With
x: Integer , we may thus writea: Rational == x; b: Rational := square x + 3; -
During assignments:
b: Rational := x; b := x * x; -
When returning from a function:
f (x: Integer): Rational == x + 1; g (x: Integer): Rational == { if x >= 0 then return x; else return 1/x; } -
Inside the
for -in construct:for x: Rational in 1 to 10 do mmout << x << " -> " << 1/x << lf;
5.2.Explicit conversions
Except for the above special cases,
|
Nevertheless, using the mechanism of parametric overloading, we may
define
|
Here
|
The new version of
The above way of adapting function declarations so as to accept
convertable arguments is so common that
|
We call this mechanism a priori type conversion of function arguments.
A similar syntax may be used for a posteriori type conversion of the return value:
|
This definition is equivalent to
|
where
|
5.3.On the careful use of type conversions
The mechanisms of a priori and a posteriori type conversions are powerful, but one should be careful not to abuse them. For instance, at a first sight, it may be tempting to allow for a priori type conversions for all routines on rational numbers:
|
Indeed, this would immediately give us support for the notation
Besides the semantic correctness issue, there is also a performance issue: the compiler has to examine all possible meanings of ambiguous expressions and then determine the preferred ones among them. It is therefore better to reduce potential ambiguities as much as possible beforehand. In the above case, this can for instance be achieved by using the following declarations instead:
|
In order to avoid the same kind of ambiguity as in the
|
In fact, most converters of a type
|
Indeed, besides the fact that we eliminate all possible ambiguities in
this way, the above routines also admit more efficient
implementations. In a similar way, for container types such as
|
The compiler has been optimized so as to take advantage of the reduced amount of ambiguities when overloading operations in this way. This should lead to an appreciable acceleration of the compilation speed, provided that the programmer adopts a similar style when using the mechanism of a priori type conversions.
6.Conditional overloading
6.1.Conditional overloading of constant functions
Until now, we have only considered overloading based on the types of expressions. The mechanism of conditional overloaded allows us to overload functions based on dynamically evaluated conditions on values. Let us start with the simple example of Fibonacci numbers:
|
This example can be reimplemented using the mechanism of conditional overloading as follows:
|
The idea here is to first specify a general implementation of the function, which can later be adapted to special cases. The overloaded versions of the function are potentially parts of other files.
In general, the syntax for a conditionally overloaded function declaration is
|
where  ,
,  ,
,
|
In the case when the function was not declared before, the function
|
be the sequence of all conditionally overloaded declarations of the
same function symbol
|
A similar remark applies in the case of function templates.
6.2.Conditional overloading of mutable functions
The mechanism of conditional overloading also applies in the case of mutable functions, but with a slightly different semantics. The general syntax for a conditionally overloaded mutable function declaration is
|
In the present case, such a declaration is equivalent to
|
At initialization,
-
Nothing prevents the user to modify the value of
fun elsewhere in the program; after all,fun is a mutable variable. -
In the case when the conditionally overloaded mutable function declarations are spread over several files, the current value of the mutable function is stored in a unique global variable which is common to all files. In particular, its value does not depend on the context, and only depends on the order in which the various files in the project are initialized (and on any other assignments of the mutable function that might occur; see the previous point).
Let us illustrate this difference with an example. Assume that we have four files a.mmx, b.mmx, c.mmx and d.mmx with the following contents:
- a.mmx
-
f (i: Int): Int == 1; - b.mmx
-
include "a.mmx"; f (i: Int | i = 2): Int == 2; b (): Void == mmout << [ f 1, f 2, f 3 ]; - c.mmx
-
include "a.mmx"; f (i: Int | i = 3): Int == 3; c (): Void == mmout << [ f 1, f 2, f 3 ]; - d.mmx
-
include "b.mmx"; include "c.mmx"; b(); c();
Execution of the program d.mmx yields
[ 1, 2, 1 ] [ 1, 1, 3 ]
If we replace
[ 1, 2, 3 ] [ 1, 2, 3 ]
In other words, in the first case, each individual file is only aware
of the overloaded declarations that occurred in the file itself and in
all recursively included files. In the second case,
In an interactive editor such as TeXmacs, conditional overloading of mutable functions is very useful, because we may use it to customize the behaviour of common editing actions as a function of the context. For instance, key presses might be handled by a global function
|
Handlers for particular keys may then be defined whereever appropriate
|
Similarly, special behaviour may be defined inside particular contexts. For instance, in a computer algebra session, pressing “enter” should evaluate the current input:
|
Of course, attention should be paid to the declaration order: the most general routines should be declared first if we don't want them to be overridden.
6.3.Conditional overloading of function templates
The conditional overloading mechanism also applies to (constant) function templates. The syntax for a conditionally overloaded function template declaration is
|
Mutable function templates are not supported.
6.4.Performance issues
In case of the mechanisms of discrete and parametric overloading, the actual resolution of the overloaded expressions (that is, the process of assigning disambiguous meanings to all subexpressions) is done during the compilation phase. This makes this kind of overloading very efficient: no matter how many times a function is overloaded, applying the function to actual values is as efficient as if the function were overloaded only once.
The mechanism of conditional overloading is more dynamic: the conditions under which a particular code gets executed are tested only at run time. Although the mechanism offers some flexibility that cannot be provided by purely static overloading mechanisms, the programmer has to be aware of this potential performance penalty. We also notice that some of the mechanisms for pattern matching to be described in the chapter on abstract data types rely on conditional overloading, and may thus suffer from a similar performance penalty.