Why develop or learn yet another programming language? At the start of the Mathemagix project during the late nineties, the state of the art concerning computer algebra systems was unsatisfactory at least for two reasons:

• There were no high quality general purpose free computer algebra systems.

• With the notable exception of Axiom and Aldor, there were no computer algebra system with a language that could be compiled.

In the beginning, the Mathemagix language was very much inspired by Axiom and Aldor, but as our ideas and implementations evolved, there were more and more differences. When Axiom and Aldor ultimately became free, our project had reached a stage in which it was interesting to further develop these new ideas.

In its present state, Mathemagix is a strongly typed functional language for computer algebra and computer analysis, which can both be intepreted and compiled. Strong typing means that every expression in the language admits a unique type, including the types themselves. For instance, the types of 2 and "hello" might be Integer and String, the type of the function (x:Integer) :-> (x*x:Integer) would be Integer -> Integer, and the type of Integer would be Class. A language is said to be functional if functions can be treated as basic objects on the same level as, say, numbers.

The requirement that programs be strongly typed has its pros and cons. On the one hand, it puts some burden on the user, since the user must carefully specify the type of every newly introduced symbol. For instance, evaluation of the expression x*y in a shell session will not work directly, since we first have to specify the types of x and y. Also, there may be some loss of flexibility. For instance, in more classical computer algebra systems, it is easy to construct vectors with entries of different types, such as [ 2, "hello", x+y ]. In Mathemagix, such expressions will only make sense if the entries can be casted into a common supertype.

On the other hand, specifying clean types for all newly introduced notations makes the semantics of the language far more robust and simplifies the task of writing compilers for the language which transform the source code into highly efficient executables. For instance, what do we actually mean by an expression such as x*y? Is this just a symbolic expression or rather an element of the polynomial ring ? Is the multiplication necessary commutative, or not? Clean typing of all declarations is a way to make potential implicit assumptions of this kind more explicit. The increased robustness in the semantics makes it also easier to develop large mathematical libraries.

Furthermore, whereas the memory layout of data can only be determined at run time for untyped languages, this kind of information and other assumptions on data are available at compile time in strongly typed languages. This opens the route to all kinds of optimizations which usually make strongly typed languages one order of magnitude faster than their untyped homologues. This is particularly important in the case of Mathemagix: besides symbolic and algebraic objects, we are also interested in the manipulation of objects of a more analytic natures, such as the numeric integration of differential equations. In order to be competitive with standard numerical libraries, an optimizing compiler is a prerequisite.

Why did we not chose for an existing strongly typed language with an optimizing compiler? There are a certain number of more traditional languages which we have considered. First of all, there are the languages OCaml, Haskell, and more recently Scala, which all belong to the family of so called ML-style languages. We also mentioned the Axiom and Aldor systems which are based on different paradigms. Other well-known languages which we considered are C++ and Scheme.

In section 2 of our paper “Overview of the Mathemagix type system”, we have outlined our main motivations for developing a new language. To go short, we want a language which adequately reflects the overloading present in traditional mathematical notation. For instance, depending on the context, the operator acts on numbers, polynomials, matrices, etc.

Conceptually speaking, we also believe that the prototype of a function declaration is analogous to a mathematical definition or the statement of a mathematical theorem, whereas the the implementation of the function is analogous to giving a proof. The type system of Mathemagix intends to make the declarations of function prototypes as precise as “operational part” of the statement of a mathematical definition or theorem. One simple example of this guiding principle is the following declaration of the cube function:

forall (R: Ring) cube (x: R): R == x*x*x;

This declaration clearly corresponds to a mathematical definition:

Definition. Given a ring , and an element 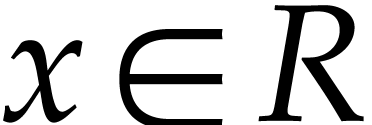, we define the cube of 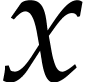by .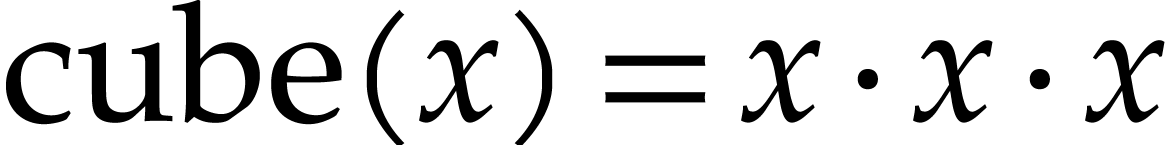

Notice that this is far more precise than simply declaring cube(x) == x*x*x. Similarly, the declaration of the function

forall (R: Real_Closed_Field)
complex_roots (p: Polynomial R): Vector Complex R == {
  …
}

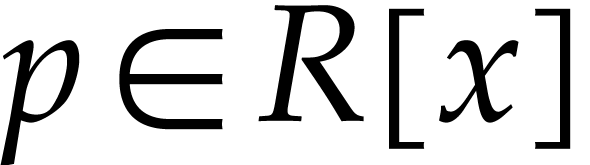corresponds to the mathematical theorem that for any real closed field and any polynomial , we may compute the vector of all complex roots of . Although this declaration is precise enough from the operational point of view, we may actually refine the prototype as follows:

forall (R: Real_Closed_Field)
complex_roots (p: Polynomial R): (v: Vector Complex R | #v = deg p) == {
  …
}

This refinement would correspond to the mathematical statement that 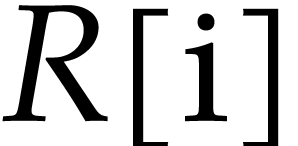is algebraically closed (and that we may actually compute the roots of polynomials). However, Mathemagix is only intended to be a compiler and not a mathematical theorem prover. Therefore, the mathematical property #v = deg p will not be rigourously proven, but only verified to hold for concrete inputs.