The dual of the polynomial ring |
The dual polynomials are represented as an ordered list of monomials, which define the inverse system associated to the polynomial ring. The corresponding type is Polynomial MonomialDualRing C, where C is the type of coefficients. Here we describe the main functionnalities available for these polynomials.
Mmx]
use "realroot"
1.Ring constructors
Mmx]
R := ZZ['x,'y]

Mmx]
D := dual R

Mmx]
Dual polynomial constructors |
|||||||
Construction of dual elements from strings:
Mmx]
l1 := D<<"215*x^4+10*x-3232231"
Mmx]
l2 := polynomial(D,"3*x^3*z-x^2*y+2")
Mmx]
|
Arithmetic operations |
|||||||||
Arithmetic operations inherited from the coefficient ring are available:
Mmx]
l1+33455552
Mmx]
l1+=l2
Mmx]
l1*l2
Mmx]
|
Functions |
||||||||||
Coefficients with respect to variable
Mmx]
coefficients(l1,0)
Coefficients of all the monomials:
Mmx]
coefficients(l1)
Differentiation with respect to variable
Mmx]
|
External product with polynomials |
|||||||||
Mmx]
p := R<<"x^2-x*z+y^3-1"
Mmx]
l1*p
Mmx]
p*l1
Mmx]
|
Mmx]

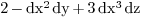



 :
:
 Dead
Dead



