The default representation for polynomials is the sparse representation corresponding to the following ring construction:

Here we define a polynomial from a string in the ring R:

In this representation only the non-zero coefficients are stored:

To manipulate dense (multivariate) polynomials, one can use the following ring construction:

The same polynomial is constructed in this ring as:

or from s as:

Now we list, the coefficients of all its monomials up to its degree, even those which are zero:

The Bernstein basis over the interval can also be used:

Notice that even if the polynomial has integer coefficients in the monomial basis, its representation in the Bernstein basis may have rational coefficients. That is why we change the coefficient field, using the ring of rational numbers.

We list the coefficients of the polynomial in the Bernstein basis:

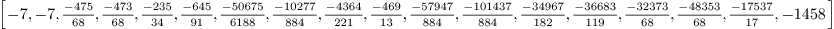Here are the coefficient of the square of this polynomial:

Univariate solvers are using the dense monomial representation. Here we output intervals with rational bounds, which contain exactly one real root of the polynomial. The precision we require on this approximation is :

We can also approximate the roots. The default bit precision which is used by the function solve_approx is the precision given by:

Here we increase the precision to get 1OOO exact bits on the numerical approximation of the roots: