Multivariate Bernstein Subdivision solver |
We consider here the problem of computing the solutions of a polynomial system

in a box 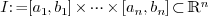 . This solver uses the representation
of multivariate polynomials in the Bernstein basis, analysis of sign
variations and univariate solvers to localise the real roots of a
polynomial system. The output is a set of small-enough boxes, which
may contain these roots.
. This solver uses the representation
of multivariate polynomials in the Bernstein basis, analysis of sign
variations and univariate solvers to localise the real roots of a
polynomial system. The output is a set of small-enough boxes, which
may contain these roots.
By a direct extension to the multivariate case, any polynomial 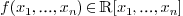 of degree
of degree  in the variable
in the variable
 , can be decomposed as:
, can be decomposed as:
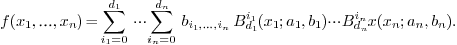
where 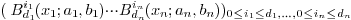 is the tensor product Bernstein basis on
the domain
is the tensor product Bernstein basis on
the domain 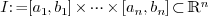 and
and  are the
control coefficients of
are the
control coefficients of 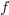 on
on  .
The polynomial
.
The polynomial 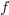 is represented in this basis by
the
is represented in this basis by
the 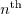 order tensor of control coefficients
order tensor of control coefficients 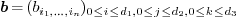 . The size of
. The size of  , denoted by
, denoted by
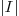 , is
, is 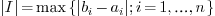 .
.
De Casteljau algorithm also applies in each of the direction  , ,
, , 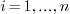 so that we can split this
representation in these directions. We use the following properties to
isolate the roots:
so that we can split this
representation in these directions. We use the following properties to
isolate the roots:
 and
and 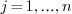 , let
, let
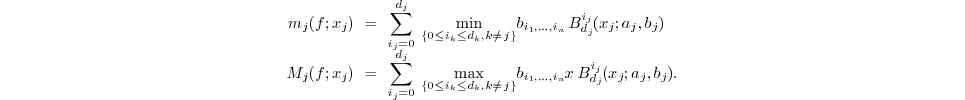
 ,
and any
,
and any 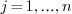 , we have
, we have
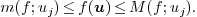
As a direct consequence, we obtain the following corollary:
 of the equation
of the equation 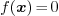 in the domain
in the domain 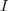 , we have
, we have 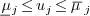 where
where
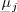 (resp.
(resp. 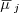 ) is
either a root of
) is
either a root of 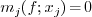 or
or 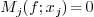 in
in 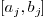 or
or  (resp.
(resp.
 ) if
) if 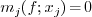 (resp.
(resp.
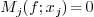 ) has no root on
) has no root on 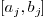 ,
,
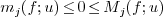 on
on 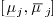 .
.
The solver implementation contains the following main steps. It consists in
- 1
-
applying a preconditioning step on the equations;
- 2
-
in reducing the domain;
- 3
-
if the reduction ratio is too small, to split the domain
until the size of the domain is smaller than a given epsilon.
As we are going to see, we have several options for each of these steps, leading to different algorithms with different behaviors, as we will see in the next sections. Indeed the solvers that we will consider are parameterized by the
-
Preconditioner: A transformation of the initial system into a system, which has a better numerical behavior.
-
Reduction strategy: The technique used to reduce the initial domain, for searching the roots of the system.
-
Subdivision strategy: The technique used to subdivide the domain, in order to simplify the forthcoming steps, for searching of roots of the system.
Preconditioners.
Solving the system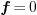 is equivalent to solving the system
is equivalent to solving the system 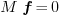 ,
where
,
where  is an
is an  invertible
matrix
invertible
matrix
As such a transformation may increase the degree of some equations, with respect to some variables, it has a cost, which might not be negligible in some cases.
Moreover, if for each polynomials of the system not all the variables are involved, that is if the systems is sparse with respect to the variables, such a preconditioner may transform it into a system which is not sparse anymore. In this case, we would prefer a partial preconditioner on a subsets of the equations sharing a subset of variables.
The following preconditioners are curently avialable:
-
Global transformation: We minimise the distance between the equations, considered as vectors in an affine space of polynomials of a given degree.
-
Local straightening: In this part we consider square systems, for which
 .
.
If we are “near” a simple solution of the system
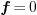 , we transform locally the system
, we transform locally the system 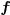 into a system
into a system 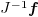 , where
, where  is the Jacobian matrix of
is the Jacobian matrix of 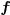 at a point
at a point  of the domain
of the domain  ,
where it is invertible. A direct computation shows that locally
(in a neighborhood of
,
where it is invertible. A direct computation shows that locally
(in a neighborhood of  the level-set of
the level-set of

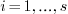 are orthogonal to
the
are orthogonal to
the  -axes. We can prove that the reduction
based on the polynomial bounds
-axes. We can prove that the reduction
based on the polynomial bounds 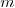 and
and  behaves like Newton iteration near a simple
root, that is we have a quadratic convergence.
behaves like Newton iteration near a simple
root, that is we have a quadratic convergence.
Reduction strategy
Here are several reduction strategies,, that can be considered.-
Convex hull reduction: A method called Interval Projected Polyhedron (or IPP) can be used in order to reduce the domain of search. It is based on the property that the convex hull property. A new reduced domain is computed, by intersecting the convex hull of the projected set of control points. With our notations, in considering the control polygons defining
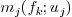 and
and 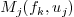 instead of these polynomials.
instead of these polynomials.
-
Extreme root reduction: A direct improvement of the convex hull reduction consist in computing the first (resp. last) root of the polynomial
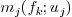 , (resp.
, (resp. 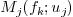 ),
in the interval
),
in the interval 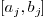 . The current
implementation of this reduction steps allows us to consider the
convex hull reduction, as one iteration step of this reduction
process.
. The current
implementation of this reduction steps allows us to consider the
convex hull reduction, as one iteration step of this reduction
process.
-
Univariate solver reduction Here, we compute all the roots of the polynomials
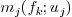 and
and 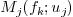 and keep the intervals
and keep the intervals 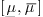 defined in
corollary ?.
defined in
corollary ?.
The guarantee that the computed intervals contain the root of
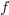 , is achieved by controlling the rounding mode
of the operations during the de Casteljau computation.
, is achieved by controlling the rounding mode
of the operations during the de Casteljau computation.
This method will be particularly interesting in the cases where more than one interval have to be considered. This may happen at the beginning of the search but is less expected locally near a single root.
Subdivision strategy
Here some simple rules that can be used to subdivide a domain. We will show in the next section their impact on the performance of the solver-
Parameter bisection: The domain
 is
then split in half in a direction
is
then split in half in a direction 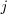 for
which
for
which  is maximal.
is maximal.
-
Image bisection: Instead of choosing the size of the interval as a criterion for the direction in which we split, we may choose a
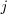 and a
and a 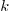 such that
such that 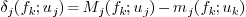 (or the difference between the
control coefficients) is maximal. Then, a value
(or the difference between the
control coefficients) is maximal. Then, a value 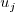 for splitting the domain in the direction
for splitting the domain in the direction 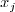 ,
is chosen
,
is chosen
-
either where
 has a local maximum,
has a local maximum,
-
or where
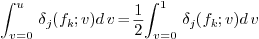
(1) The right-hand side of this equation can be easily computed, from the sum of all the control coefficients of
 .
.
-