Sleeve univariate solver |
A first family of methods correspond to the scheme. It starts with a
representation of a polynomial  (on an interval
(on an interval
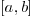 ) and according to some criterion
) and according to some criterion 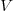 , it applies remove the interval, keep it on split it:
, it applies remove the interval, keep it on split it:
Algorithm
solve_binary(f,I)
Compute the number of sign changes
If
If
If
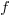 on the interval
on the interval 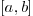 .
.
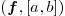 associate with
associate with 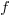 .
.
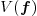 of the coefficient sequence
of the coefficient sequence  .
.
 , remove the
interval.
, remove the
interval.
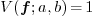 , output the
interval
, output the
interval 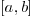 and
and 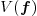 .
.
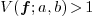 subdivide the
representation into two subrepresentations,
corresponding to the two halves of the input
interval and apply recursively the algorithm to
them.
subdivide the
representation into two subrepresentations,
corresponding to the two halves of the input
interval and apply recursively the algorithm to
them.
 .
.
Typically, one can use the representation of a polynomial  in the Bernstein basis on
in the Bernstein basis on 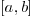 :
: 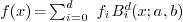 , where
, where  . The subdivision
step will be based on de Casteljau algorithm.
. The subdivision
step will be based on de Casteljau algorithm.
For 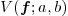 , one can take the number of sign variation
of the control coeffcients
, one can take the number of sign variation
of the control coeffcients 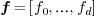 , not taking into
account the
, not taking into
account the 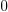 of this sequence. By Descartes'
rule, if the polynomial
of this sequence. By Descartes'
rule, if the polynomial  has no multiple root,
the algorithm outputs a list of intervals containing one and only one
root.
has no multiple root,
the algorithm outputs a list of intervals containing one and only one
root.
Two variants are implemented.
-
If we take for
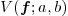 the number of sign
variation of sequence
the number of sign
variation of sequence 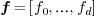 , not taking into
account the
, not taking into
account the 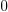 of this sequence. By
Descartes' rule, if the polynomial
of this sequence. By
Descartes' rule, if the polynomial  has no
multiple root, the algorithm outputs in this casea list of
intervals containing one and only one root.
has no
multiple root, the algorithm outputs in this casea list of
intervals containing one and only one root.
-
If we asked in addition that
 , where
, where  is the precision attached to the solver, we
approximate the roots within the precision
is the precision attached to the solver, we
approximate the roots within the precision  .
.